3.2 Squares and Square Roots
We mentioned that the A/B scales can be used for multiplication/division, as can the C/D scales. But the primary use of this complete set of scales is to quickly find squares and square roots. The length of a decade (from 1 to 10 on the scale, for instance) on the A scale is half the length of a decade on the D scale. Hence, as the logarithm of a number on D advances, the logarithm of a number on A advances at twice that rate. In other words, “log A” = 2 \(\times\) “log D” which tells us that A = D\(^2.\)
The A scale gives the squares of the numbers found on the D scale. This is very convenient when one wants to calculate areas of squares or circles, calculate kinetic energies, calculate power when given an electrical current and resistance, etc. In reverse, for a given number on the A scale its “square root” will be found directly on the D scale. The same relationship of course holds between the B and C scales as for the A and D scales. The figure below shows a close-up of the B and C scales of our example slide rule. It is easy to spot on the B scale the squares of the numbers on the C scale. Is it easy to read off the value of \(\sqrt{2}\)?

Suppose we wish to calculate the kinetic energy \(W\), in Joules, of an object of mass \(m\) = 2.7 kg moving at a speed \(v\) = 6.8 m/s. The formula for kinetic energy is \(W = \frac12 mv^2\). Let’s do the calculation two different ways. First, we can use the C/D scales to multiply all the factors together:
- Line up the cursor to 5 on the D scale.
- Align 10 on the D scale with the cursor, and move the cursor to 2.7 on the C scale.
- Align the 1 on the D scale with the cursor, and move the cursor to 6.8 on the C scale.
- Align the 10 on the D scale with the cursor, and move the cursor to 6.8 on C again.
- Find the result at the cursor on the D scale: 6.25.
- Estimate the answer: a bit less than 3/2 \(\times\) 49 \(\approx\) 75.
- So, final answer should be 62.5 Joules.
The above calculation took three settings of the slide. Alternatively, we can calculate the result with a single setting of the slide (in this particular case) utilizing the A scale. Start by placing the cursor on 2.7 on the A scale. Then, move the slide to line up the 2 on the B scale with the cursor. The result of dividing 2.7 by 2 will be found on the A scale, aligned with the 1 on the B scale. But note that the square root of this result is also found directly below on the D scale. Since the 1 on the C scale is also aligned with this result, we can now multiply by 6.8 by moving the cursor to 6.8 on the C scale. At this point we have on the D scale – under the cursor – the result of \(\sqrt{m/2}\times v\). The square of this number will be directly above on the A scale. It should read roughly \(\frac12 mv^2\) = 62.5 (Joules) and is our final answer.
Yet again, via computer:
## [1] 1/2 * 2.7 * 6.8^2 = 62.424 JNotice, too, that the kinetic energy for other speeds as well, from 1 m/s up to about 8.6 m/s, can be read without having to move the slide.
Here is another way to look at what is happening in this operation. We are using the A and B scales to perform a basic calculation. We find 2.7 on A, and divide by 2, to get 1.35 on the A scale. Next, we want to multiply by 6.8 squared. We do this by placing the left index on B to 1.35 on A using the cursor. Then we want to move the cursor to the right by an amount on B that is equal to 6.8 squared. Well, directly below B is the scale C. The value of 6.8 on C is the same distance away from the left index as is the value of \(6.8^2 = 46.2\) on B, exactly what we need. So we move the cursor to 6.8 on C, equal to \(6.8^2\) on B, which gives us our final result on A.
Another common calculation is that of the length of the hypotenuse \(c\) of a right triangle given the lengths of the other two sides, \(a\) and \(b\), where \(c^2 = a^2 + b^2\). Suppose two sides have lengths \(a\) = 3.7 and \(b\) = 5.2 and we want to calculate \(c\). One way is to use the A scale and find the square of \(a\) (13.7) and the square of \(b\) (27), and – writing down the results if necessary – add the two results together (40.7). Then, move the cursor to this result on the A scale and find its square root directly below on the D scale: about 6.35.
Another approach is to rewrite the relationship as \[ c = \sqrt{a^2 + b^2} = a\sqrt{1+(b/a)^2} \] where we note that \(b>a\) for the computation that follows. This time, using just two settings of the slide and without having to write down any intermediate results, we can find the hypotenuse. Here are the steps to perform on the slide rule:
- Move the cursor to 5.2 on the D scale.
- Align 3.7 on the C scale to the cursor, thus dividing 5.2 by 3.7 (= \(b/a\)).
- Sliding the cursor to the 1 on the C scale, we follow the cursor to the A scale to read the square of this result: 1.98 (= \((b/a)^2\)).
- Mentally adding 1 to the result, we move the cursor to 2.98 on the A scale, \(1+(b/a)^2\).
- The square root of the present result will be directly below on the D scale, \(\sqrt{1+(b/a)^2}\); so next we move the slide to align the 1 on the C scale with the cursor.
- Moving the cursor to 3.7 on the C scale we are multiplying the previous result by 3.7 (\(a\)).
- The final answer, \(c=a\sqrt{1+(b/a)^2}\), will be at the cursor on the D scale: \(c\) = 6.38.
Check:
## [1] sqrt( 3.7^2 + 5.2^2 ) = 6.38200595424354
As a matter of fact, the same technique for the hypotenuse calculation can be made with only one setting of the slide. Take one number, say the larger one \((b)\), and find it on D. Line up the middle index on B (the “10”) with this number. Then, using the cursor, find the second number \((a)\) on D. Read off the number under the cursor that is now found on B; call this \(n\). Then, slide the cursor over to the number “\(n + 10\)” on the B scale. Under the cursor on D will be \(\sqrt{a^2 + b^2}.\) Let’s apply this to our specific example:
- Move the cursor to 5.2 on the D scale.
- Align the middle index on B to the cursor.
- Now find 3.7 on the D scale using the cursor.
- Read the number \(n\) under the cursor on B. It should be \(n\) = 5.05.
- Move the cursor to \(n+10\) = 15.05 on the B scale.
- remember to interpret the middle index as “10” on B, and then find 15.05
- remember to interpret the middle index as “10” on B, and then find 15.05
- Under the cursor, on D, read the answer: \(\sqrt{5.2^2 + 3.7^2}\) = 6.38.
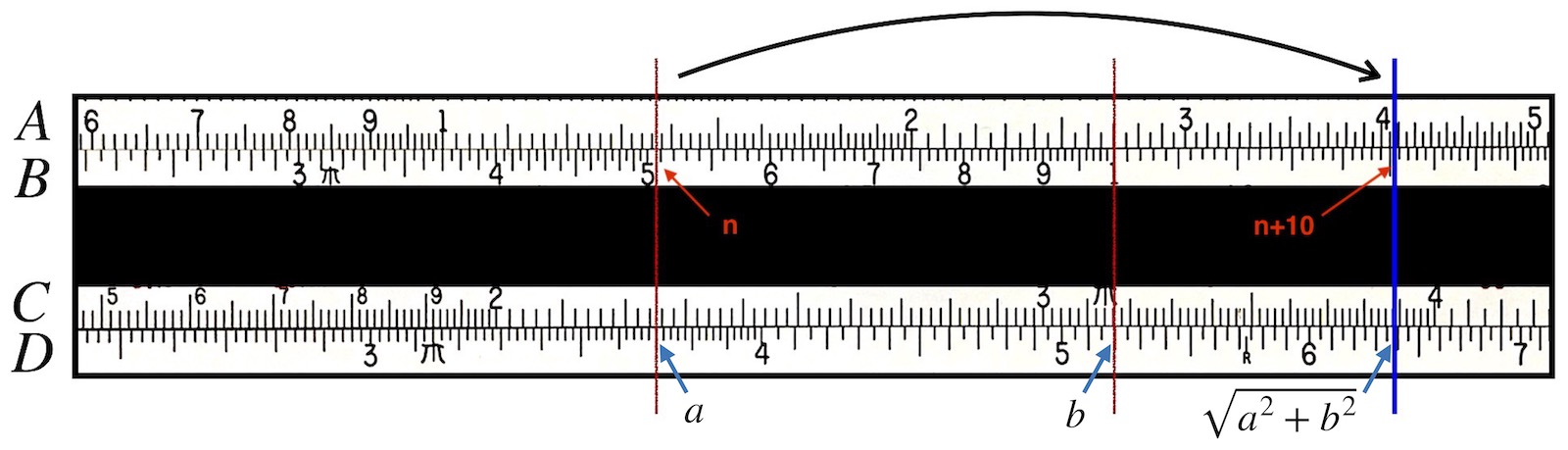
This last example is actually an old technique, best arrived at by the law of proportions. (See discussions found in the vignettes entitled Out of Proportions and Carpenters vs. Engineers, particularly, Comments on Scale Development.) It was more commonly taught in Europe, while our preceding method more likely would have been taught in the U.S. schools during the mid-20th century. So how does this work? The numbers on the A/B scales are squares of the numbers on the C/D scales, and hence if we line up a number \(N_B\) on B with a number \(N_c\) on C this corresponds to a ratio of \(\sqrt{N_B}/{N_C}.\) With the slide set in this position, all other numbers on B and C are set to the same ratio.
So, for instance, in our figure above, the slide is set to this common set of proportions:
\[ \frac{\sqrt{n}}{a} = \frac{\sqrt{10}}{b} = \frac{\sqrt{n+10}}{x} \]
and we would like to solve for \(x\) by eliminating \(n\) from these equations. Take the first and second ratios; they give \(n = 10(a/b)^2\). Hence, the second and third ratios give us
\[ \frac{\sqrt{10}}{b} = \frac{\sqrt{10(a/b)^2+10}}{x} = \frac{\sqrt{10}\sqrt{(a/b)^2+1}}{x}; \]
Dividing by \(\sqrt{10}\) and re-arranging gives us
\[ x = b\sqrt{(a/b)^2+1} = \sqrt{a^2+b^2} \]
and there we have it!