1.4 Keeping Track of Decimal Places
Consider the numbers 3.7, 37, and 370. Using our rules for logarithms, we see that each power of ten adds “one” to the value of the logarithm:
\[\begin{eqnarray*} \log 3.7 &=& \log (3.7\times 1) &=& \log 3.7 + \log 1 &=& \log 3.7 + 0 \\ \log 37 &=& \log (3.7\times 10) &=& \log 3.7 + \log 10 &=& \log 3.7 + 1 \\ \log 370 &=& \log (3.7\times 100) &=& \log 3.7 + \log 100 &=& \log 3.7 + 2 \\ \end{eqnarray*}\]
We can see a similar pattern when looking back at our table of logarithms above. For example, notice that \(\log 6\) = 0.7782, while \(\log 60\) = 1.7782. By keeping track of powers of 10, one only needs the values of the logarithms for numbers between 1 and 10 to be able to determine the logarithm of any other number outside that range.
As an illustration, recall the plot we made earlier using Base 2. The pattern between each integer value of \(p\) repeats; the corresponding point in each repeat section is just “2” times larger than the point in the previous section of the plot:
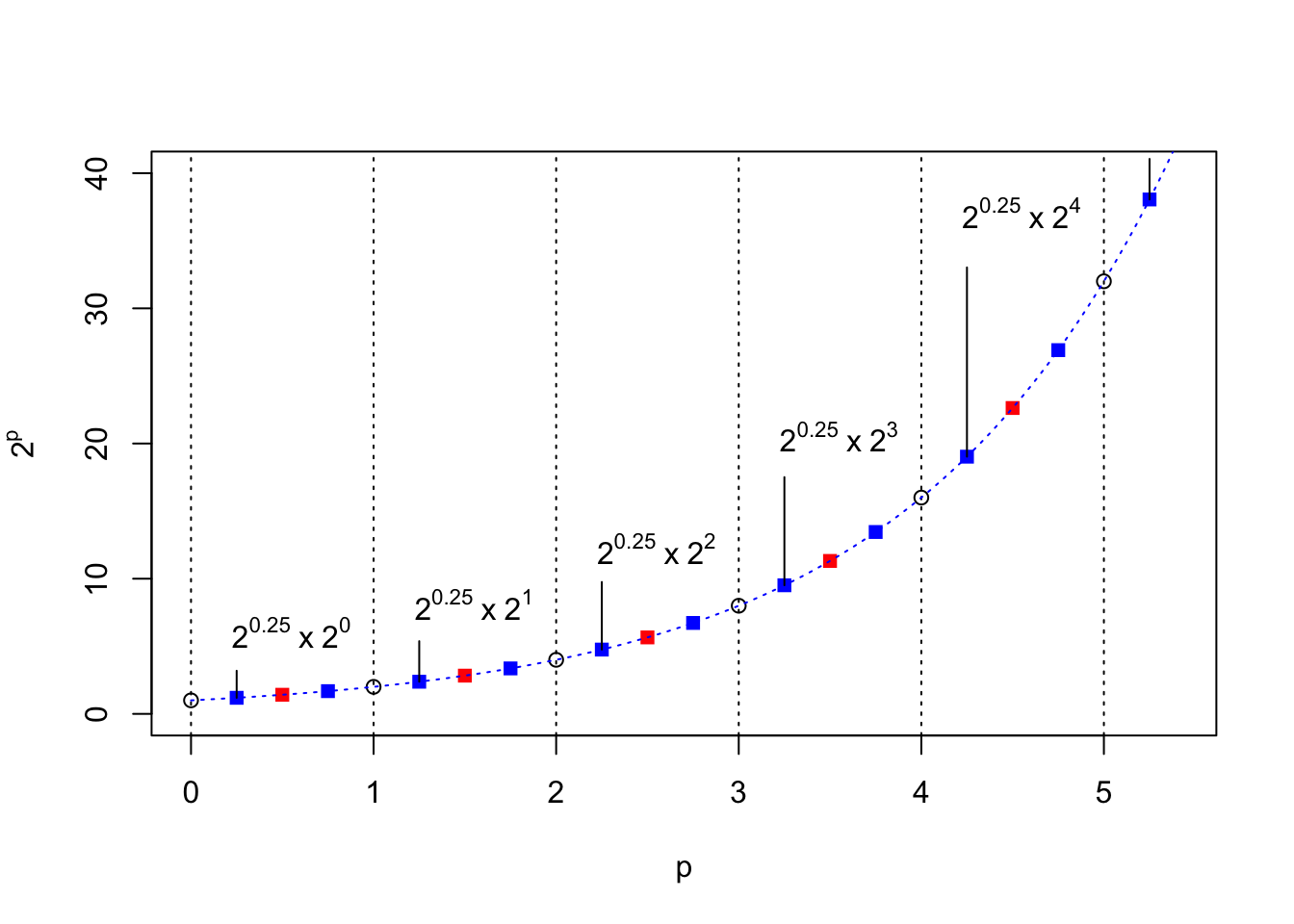
Hence, if we want to know the value of \(2^{7.25}\), we only need to know the value of \(2^{0.25}\) and then multiply this answer by \(2^7\) (= 128).
We can use any number as our base, and the same general rules will apply; for our Base 10 system of common logarithms, multiplying by factors of 10 simply means adding zeroes or moving decimal points. As a matter of fact, this was a primary reason that Napier and Briggs decided to use “10” as the base of their logarithm table. And, by the way, for the purpose of keeping track of the powers of ten, Napier invented the “decimal point”. So, with this technique, detailed tables of common logarithms of numbers between 1 and 10, which themselves will have values between 0 and 1, are sufficient to perform a fairly accurate general multiplication or division calculation, as we shall soon see.
For example, the table below gives the 3-place logarithms for numbers between 1 and 10 in increments of 0.1. For finer increments and for further accuracy of the logarithms, tables can take many pages of text. This led to the publication of books of significant length that contained detailed tables of logarithms. But for now, consider the following:
| x | Log(x) | x | Log(x) | x | Log(x) | x | Log(x) |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 3.3 | 0.519 | 5.6 | 0.748 | 7.9 | 0.898 |
| 1.1 | 0.041 | 3.4 | 0.531 | 5.7 | 0.756 | 8 | 0.903 |
| 1.2 | 0.079 | 3.5 | 0.544 | 5.8 | 0.763 | 8.1 | 0.908 |
| 1.3 | 0.114 | 3.6 | 0.556 | 5.9 | 0.771 | 8.2 | 0.914 |
| 1.4 | 0.146 | 3.7 | 0.568 | 6 | 0.778 | 8.3 | 0.919 |
| 1.5 | 0.176 | 3.8 | 0.58 | 6.1 | 0.785 | 8.4 | 0.924 |
| 1.6 | 0.204 | 3.9 | 0.591 | 6.2 | 0.792 | 8.5 | 0.929 |
| 1.7 | 0.23 | 4 | 0.602 | 6.3 | 0.799 | 8.6 | 0.934 |
| 1.8 | 0.255 | 4.1 | 0.613 | 6.4 | 0.806 | 8.7 | 0.94 |
| 1.9 | 0.279 | 4.2 | 0.623 | 6.5 | 0.813 | 8.8 | 0.944 |
| 2 | 0.301 | 4.3 | 0.633 | 6.6 | 0.82 | 8.9 | 0.949 |
| 2.1 | 0.322 | 4.4 | 0.643 | 6.7 | 0.826 | 9 | 0.954 |
| 2.2 | 0.342 | 4.5 | 0.653 | 6.8 | 0.833 | 9.1 | 0.959 |
| 2.3 | 0.362 | 4.6 | 0.663 | 6.9 | 0.839 | 9.2 | 0.964 |
| 2.4 | 0.38 | 4.7 | 0.672 | 7 | 0.845 | 9.3 | 0.968 |
| 2.5 | 0.398 | 4.8 | 0.681 | 7.1 | 0.851 | 9.4 | 0.973 |
| 2.6 | 0.415 | 4.9 | 0.69 | 7.2 | 0.857 | 9.5 | 0.978 |
| 2.7 | 0.431 | 5 | 0.699 | 7.3 | 0.863 | 9.6 | 0.982 |
| 2.8 | 0.447 | 5.1 | 0.708 | 7.4 | 0.869 | 9.7 | 0.987 |
| 2.9 | 0.462 | 5.2 | 0.716 | 7.5 | 0.875 | 9.8 | 0.991 |
| 3 | 0.477 | 5.3 | 0.724 | 7.6 | 0.881 | 9.9 | 0.996 |
| 3.1 | 0.491 | 5.4 | 0.732 | 7.7 | 0.886 | 10 | 1 |
| 3.2 | 0.505 | 5.5 | 0.74 | 7.8 | 0.892 |
One can immediately see how logarithms can be used to multiply numbers. For example, notice from our table that the logarithm of 1.5 is 0.176 and the logarithm of 3.6 is 0.556. The sum of the logarithms is 0.732, which we can see from the table is the logarithm of 5.4 = \(1.5\times\) 3.6. Clearly many other examples can be found just from this simple table. Now suppose we wanted to multiply \(150\times\) 3.6. We don’t need to have the logarithm of 150 in our table – the logarithm of 150 will just be 2 + the logarithm of 1.5, or 2.176. The number with that logarithm will just be \(10^2\) times the result for \(1.5\times\) 3.6, or 540. By keeping track of powers of ten, calculations can be performed by just using logarithms of numbers between 1 and 10.