8.38 Slide Rules for the Sikes Hydrometer
Latest Update: 2024 Aug 29
Originally posted: 2023 Apr 22
The hydrometer is an instrument that dates back to the days of Archimedes (3rd century BC), the Greek philosopher famous for the interpretation of the buoyancy of items in water. In particular, his principle accurately describes how an item can float on or in water without sinking, for example how a large, heavy ship can possibly float on the surface of the ocean. The hydrometer is an instrument based upon this principle and which is used to determine the density, or specific gravity, of a liquid compared to the density of water. Its use in our context is in the determination of the percentage of alcohol present in a liquid sample of whisky and other spirits, for example. Such measurements of the specific gravity of an alcoholic beverage have been used for centuries to assess taxes on such liquids. And starting with the English, special slide rules began being used for such calculations in the 1600s.
8.38.1 Buoyancy and Archimedes’ Principle
An item is deemed “buoyant” if it is able to stay afloat or able to float toward the surface of a liquid. To understand buoyancy, consider the interface between a liquid and air. If the system is in equilibrium, then the pressure exerted at this interface is equal in both directions, and must be equal to the local air pressure (typically about \(P_0\) = 14.7 pounds per square inch in “English” units). However, if one pushes an object to a point below the surface, the pressure from the surrounding liquid will increase with the depth:
\[ P = P_0 + \rho g h \]
where \(\rho\) is the density of the liquid, \(g\) = 32 feet per second per second is the local acceleration due to gravity, and \(h\) is the depth in question. As a result, if a solid object is placed in the liquid then the pressure on all parts of the object is governed by the above relationship, and the total upward force due to the pressures on all parts of the object will sum up to the so-called buoyant force. If need be these forces might rotate the object around until all of the “horizontal” forces are balanced. But, once these horizontal forces are in equilibrium, if the buoyant force upward is greater than the weight of the object, then it will float upward. The final upward forces due to the pressure of the liquid will be determined by how much liquid is displaced by the object. The more liquid that is displaced, the more total pressure will be on the object and the larger the buoyant force. If an object floats at the surface, perhaps partially submerged, then the weight of the displaced liquid will be exactly the total weight of the object. This is Archimedes’ Principle.
As an example, consider a solid rectangular metal box with square bottom and top being lowered into a liquid, as depicted in the figure below. The material of the box itself has total weight of \(W_b\), but its inside is only filled with air. The cross-sectional area at the top and bottom of the box is \(A\). The box is found to float in the water when the bottom of the box is at a depth \(h\). The box has pressure on all sides, and this pressure varies with depth. However, for every point on the left side, say, where the pressure exerts a force to the right, there is an equal point on the right side where the pressure exerts a force to the left. These cancel each other out. Since there is only air on either side of the top surface, the forces here of the air on each side also cancel each other. The only remaining force to consider is at the bottom of the box.
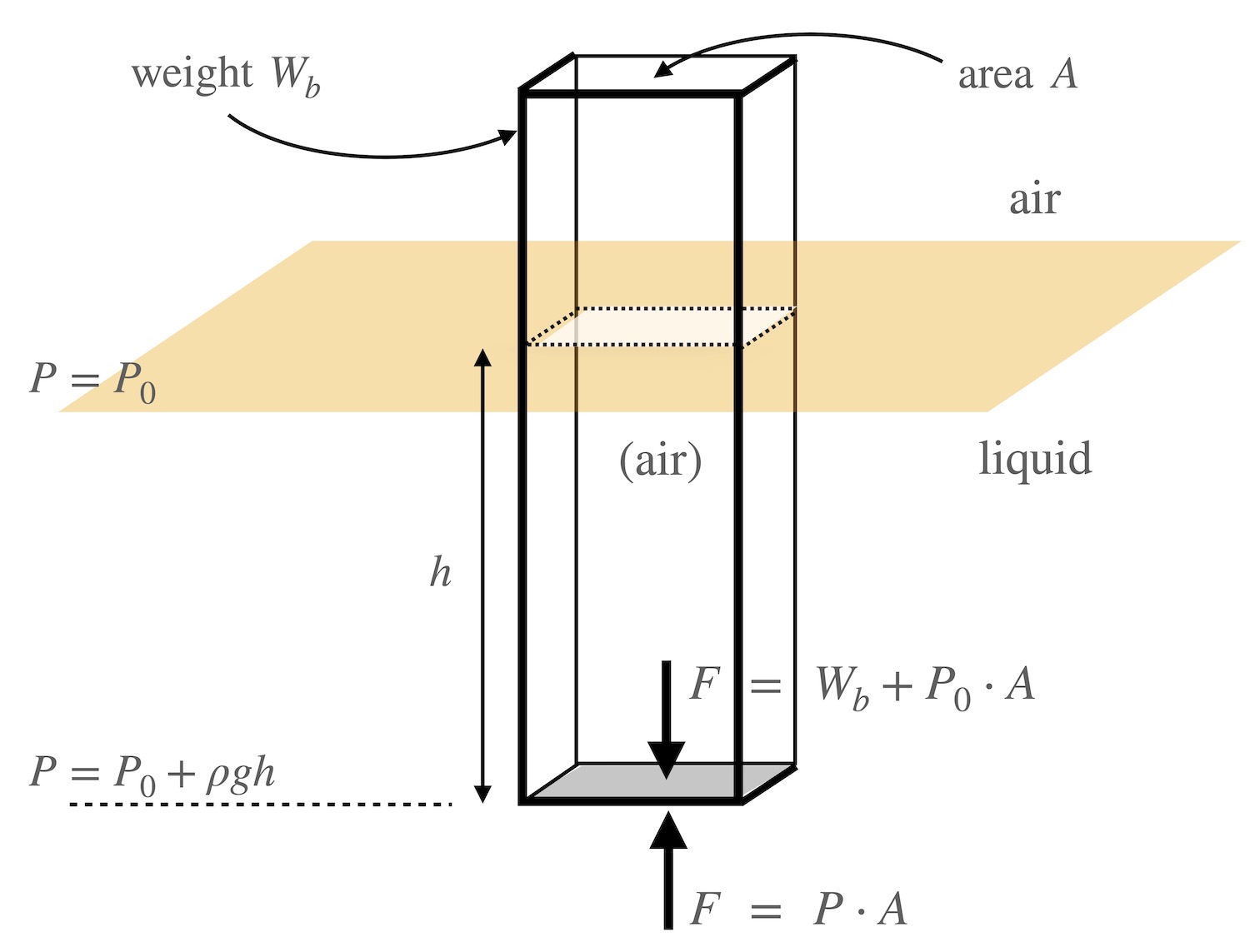
At the bottom surface of the box, the pressure of the water pushing upward is \(P = P_0 + \rho g h\) and so the force upward on the container will be \(F = P\cdot A\) = \(P_0A + \rho g h A.\) The force acting downward on the bottom of the box will be that of the weight of the container plus the force from the air pressure \(P_0\) across the surface \(A\), i.e. \(F = W_b + P_0\cdot A\). Since the object in question is in equilibrium (that is, it is “floating” in a stationary position) then these two forces must be equal and hence \(P_0A + \rho g h A\) = \(W_b + P_0A\), or
\[ \rho\; g \cdot h \cdot A = W_b. \]
Note that \(h\cdot A\) is just the volume of liquid that has been displaced by the box. For an object of a given weight, a box of smaller cross-section (smaller \(A\)) will sink deeper (larger \(h\)). And a box of constant cross section and weight will sink deeper in a less dense liquid, or sink less in a more dense liquid.
The above calculation assumed a rectangular box; however, the result can be shown to be independent of the shape of the object. As we said above, an arbitrary floating object will re-arrange itself in the liquid until all horizontal forces are balanced; then, once in equilibrium, it will attain a depth that is dependent only upon its weight and the volume of displaced liquid. If \(V_w\) is the volume of displaced water (\(=h\cdot A\) in our example above), then the density of the liquid can be found from
\[ \rho = \frac{W_b}{gV_w}. \]
8.38.2 The Sikes Hydrometer
The hydrometer is a calibrated instrument that operates according to Archimedes’ principle. It is a hollow device designed to float in liquid in a particular orientation such that its depth can be measured consistently from outside the liquid. The hydrometer is calibrated so that it floats at a certain depth in pure water. When placed in a different liquid of different density, then the change in the depth it acquires will be determined by the difference in density of the liquid from that of water. Hydrometers were being used to ascertain the amount of alcohol in liquids in the 1600s and beyond, but it wasn’t until the early 1800s that England adopted a standard device for this use, which was the Sikes Hydrometer. In 1802 a Committee of Inquiry was appointed in England to come up with a standard hydrometer. By 1816 a competition was enacted that received nearly 20 instruments submitted by a number of makers. The design of Bartholomew Sikes was chosen as the winner.160 It remained the legal standard in England until 1907, and reportedly was still often used until around 1980.161
Below is an image of an incomplete Sikes Hydrometer set from the early 1800s. It is missing its thermometer (the density of a liquid will depend upon temperature), and one of its weights. One of the other weights evidently has been replaced in the past. This set was manufactured by Thomas Gill of London, which was in business during the years 1806-1824. Thus, the hydrometer was most likely manufactured between 1816 and 1824.


Sikes Hydrometer Set (incomplete) from c. 1820.

The most interesting feature (to me) of this particular set is that it contains two slide rules. Originally, Sikes produced a book of tables from which the results of the hydrometer measurements could be converted to “proof” levels depending upon the measured temperature of the liquid. But it did not take very long at all for slide rules to be developed which replaced the need to have the book except for very accurate determinations.


8.38.3 A typical measurement
The hydrometer has a stem on top of square cross-section that has engraved markings and numbers from 0 to 10. It also has a series of weights, labeled from 10 to 90 that can be attached to the bottom stem. The set also includes a “cap” that can fit over the top of the square stem. The cap and all of the weights are calibrated to work with the scale on the top stem. By adding weights to the bottom stem, the device can be made to float in a variety of liquids of differing density so that the liquid level can be read on the scale found on the top stem. And since the top stem is uniform in cross section, then variations in the readings can readily be turned into variations in the volume of displaced liquid.

From an 1860 publication on the use of the Sikes hydrometer:162
The line on the edge of the Stem near Division 1 is the point to which the Weight 60 sinks the Hydrometer in spirits exactly of the Strength of Proof, at \(51^\circ\) Temperature : the square weight or cap being applied at the top of the Stem will, with the above-named Weight, sink the Hydrometer to the same point in distilled water of the same Temperature; and being exactly one-twelfth part of the total weight of the Hydrometer and Weight 60, confirms the definition of Proof Spirit given in the Act of Parliament for establishing this Hydrometer, which states Sikes’s Proof Spirit to weigh at \(51^\circ\) Temperature, exactly twelve-thirteenth parts of an equal bulk of distilled water; and this cap may be at any time so employed to determine the fitness of the Instrument for use.
By adding weights to the bottom stem below the surface of the liquid, and measuring the liquid level on the upper stem, an “indication” would be deduced. From the same publication:
Bring the eye to the level of the surface of the sample, note what part of the Stem be cut by that surface, as seen from below, and add such part or Division to the number of the Weight for the INDICATION.
To understand what is going on, look at our relationship \(\rho\cdot h = W_b/(gA)\). For a constant reading on the stem, a higher “indication” value that is made by adding heavier weights means that the liquid must be of higher density. And since water is more dense than alcohol, then a higher indication number means that the concentration of alcohol, or “proof”, of the liquid is lower. Also, other parameters held constant, the reading on the stem gets higher as the hydrometer floats closer to the surface, meaning that the liquid must be more dense, and thus – again – of lower “proof”.
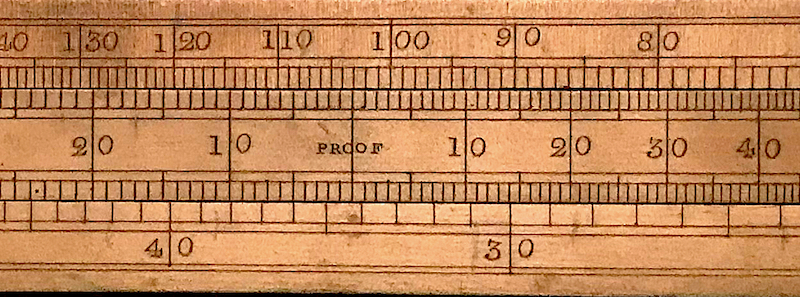
Once an “indication” was made, the first slide rule, called the Proof Slide Rule, could be used to determine the proof of the liquid. Suppose the temperature of the liquid was measured to be 58 F, and that a weight of 60 was used, while the stem reading was 7.6 (as in the illustration above). This gives an “indication” of 67.6. The index of the scale on the slide is indicated by a line with three circles above it, sometimes called the star. We set this mark on the slide rule against the temperature of 58 on the bottom scale. We then look for 67.6 on the slide; it could be on the front or the back of the rule, depending on the value being sought. In our case, 67.6 lines up against 13.8 on the front top scale. Note that this is to the right of the “PROOF” gauge mark on this scale. As mentioned above, higher indications coincide with lower proof. Thus, results to the right of the “PROOF” mark mean that the liquid is “under proof.” In our present example, the liquid is deemed to be 100 - 13.8 = 86.2 proof. Notice, too, that if we turn our rule over, the numbers on the slide represent “indications” in the range from about 14 up to about 59, most of which would correspond to “over proof” for typical temperatures. Many proof slide rules are found to have labels on the two sides of the rule with the words “Under Proof” and “Over Proof” to help avoid confusion.

8.38.4 Assessing a Tax
With the proof determined, the next stage is to assess a taxation on the liquid. This, of course, can vary from year to year according to the government rates. The tax itself is based upon the total amount of alcohol, not the total volume of any liquid, and hence the tax rate can be given as a single number – the rate for proof liquid. One can imagine a couple of ways to approach this. First, one could find the appropriate higher or lower tax rate per gallon for an over- or under-proof liquid and then multiply by the total number of liquid gallons. Or, similarly, one can find the equivalent number of gallons of proof liquid that would correspond to the same amount of alcohol in our given gallons of original liquid. This was called a reduction calculation. Then, one just multiplies this number of equivalent gallons by the standard tax rate for proof alcoholic liquids. The Comparison Slide Rule was used for these two types of calculations.
8.38.4.1 direct calculations
The numbers on one side of our Comparison rule range from 8 on the left to 42 on the right on the top scale and from about 1.5 on the left to 8 on the right on the bottom scale; the units are shillings. We align the “PROOF” gauge mark on the slide of the rule with the current tax rate for proof liquid on the stock of the rule. So, for a certain number of shillings per unit of volume of liquid, the tax rate for PROOF liquid is set, and the user can read off the tax rate for any over- or under-proof value directly from the slide rule. Then, multiplying this tax rate by the number of gallons of liquid would determine the final tax.
8.38.4.2 reduction calculations
The top scale on the other side of the Comparative Slide Rule goes from 300 on the left down to 60 on the right, and the bottom scale goes from 100 on the left down to 20 on the right. The point of this set of scales is to determine how many gallons of proof liquid would be equivalent to the number of gallons of our given liquid. Suppose we have 85 gallons of 120.2 proof liquid. We set 120.2 on the proof scale against 85 on the top scale. Then we see that this is equivalent to 103 gallons of proof liquid. We can then just charge our lucky merchant for 103 gallons times the proof tax rate.
If these two slide rules were used as described above, then a third slide rule might have been used to multiply the final tax rate with the appropriate volume of the liquid being taxed. I would presume that the excise tax officer would have a very nice, accurate standard slide rule for this final step, such as that which might be found on an Excise Officer’s Gauging Rule.