8.10 Out of Proportions
Originally posted: 2022 Dec 10
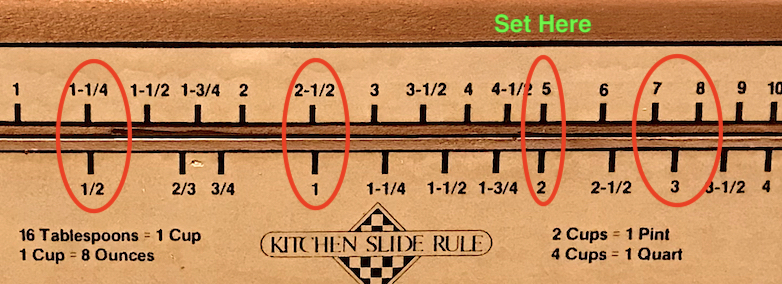
So suppose a cooking recipe you found in a magazine calls for 2 limes, 0.5 cup of sugar, 1 tablespoon of THIS and 3 ounces of THAT to produce the perfect drink that serves 2 people. So now you are going to entertain and need to prepare your concoction for a party of 5 people. What is one to do? Well, clearly you need a kitchen slide rule, like the one pictured here:

To use, align the 2 on the lower scale with the 5 on the upper scale. Now, any amount that you read on the lower scale for the recipe for 2 people is lined up on the upper scale with the amount necessary for 5 people. Reading off this single setting, it’s easy to see (below) that you need 5 limes, 1.25 cups of sugar, 2.5 tablespoons of THIS and 7.5 ounces of THAT. It doesn’t matter whether the recipe items are written in terms of ounces, or grams, or liters, or pounds of meat, or bushells of corn, it works all the same. It’s like magic! Well, actually, it’s logarithms! And the principle being used is, of course, the law of proportions.
8.10.1 Ratio Aspects
Let’s look at the aspects of finding ratios. If two quantities are always in a certain ratio, like apples to oranges, then we say that \(a\) apples is to \(b\) oranges as \(c\) apples is to \(d\) oranges; or, \(a:b\) as \(c:d\); or, equivalently, we can write
\[ \frac{a}{b} = \frac{c}{d} = {\cal R} \]
where \({\cal R}\) is the value of the ratio. If the number of apples is doubled, then the number of oranges must be doubled in order to keep the ratio between the two the same.
The act of finding equal ratios and proportions is a straightforward operation using the basic scales of a slide rule. Using a slide rule to divide two numbers is described in the Section Basic Multiplication and Division. Putting the cursor at 5 on the A scale of a standard Mannheim slide rule and moving the slide to align the 2 on the B scale under the cursor, the result is found at the 1 on the A scale: 5 divided by 2 = 2.5. In terms of ratios, we can describe the situation as
\[ \frac{5}{2} = \frac{2.5}{1} \]
where our value for \({\cal R}\) = 2.5. But now, without moving the slide, we can scan the two scales to see most of the other combinations of numbers that give this same final result. Some examples include (A/B) = (20/8, 15/6, …) and so on, as well as the combinations we are looking for: (A/B) = (5/2, 2.5/1, 7.5/3). The one combination of ours that does not show up in this fashion is (A/B) = (1.25/0.5), which falls off-scale to the left. A simple re-indexing of the slide allows for its evaluation as well. (We have more to say about this later.) And of course we see that the standard slide rules give a much more accurate set of numbers than does the simple “kitchen slide rule” above (for those discerning chefs and bartenders).

Another way to write all of this would be to say that all of the following ratios are equivalent:
\[ \frac{2~{\rm limes}}{2~{\rm people}} = \frac{5~{\rm limes}}{5~{\rm people}} ~~~~~~ and ~~~~~~ \frac{0.5~{\rm cups} }{2~{\rm people}} = \frac{1.25~{\rm cups} }{5~{\rm people}} ~~~~~~ and ~~~~~~ \ldots \] Cross-multiplying each equation above, the ratio of people in the two cases is the same as the ratio of limes and is the same as the ratio of cups and so forth – which are all equal to 5/2 = 2.5.
\[ \frac{5~{\rm people}}{2~{\rm people}} = \frac{5 ~{\rm limes} }{2~{\rm limes}} = \frac{1.25 ~{\rm cups} }{0.5~{\rm cups}} = \frac{2.5 ~{\rm tablespoons}}{1~{\rm tablespoons}} = \frac{7.5 ~{\rm ounces} }{3~{\rm ounces}} = \frac{5}{2} \]
8.10.2 Specialty Rules
The use of ratios and proportions and relevant computations as shown above are very common in many aspects of daily life, as well as in a number of professions and industries. One particular example was expounded upon in the vignette Rules of Engravement. In addition to the newspaper and printing industries, such rules can be found for use in photography enlargement/reduction, architecture, and in other arts in which an accurate scaling is required.
In our example above it was noted how one of our necessary calculations for our fictitious recipe was found “off-scale” and required a re-indexing of the slide rule being used. If, on the other hand, we had been using a circular slide rule rather than a Mannheim-style linear slide rule, then this issue would not exist. Such circular slide rules for proportions were popular during the last century, and similar items still can be found at many art supply stores today. Below is an example from the Collection of a proportional scale that had belonged to the famous comic book artist, Johnny Craig. According to his son, Steven Craig, Johnny would sometimes create an original work but then would need to make a new version scaled appropriately for the final publication, for instance. Through the use of a grid system overlaid on the original sketch, he could then use the proportional scale to generate a new scaled replica which he could then fill in and paint for final production.

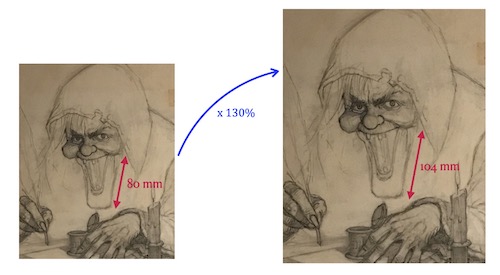
One of the special features of using a circular slide rule is that the index (the 1 or 10 or 100 on the slide rule) does not need to be “re-set” in order to read a final answer, since the pattern of the scale is the same between each decade. Hence, to scale up an image of the Vault Keeper by 30%, one can set the dial such that the Percentage of Original Size is at 130%. One should see a setting of 1 inch on the Size of Original is against a Reproduction Size setting of 1.3 inches, and so forth. Now, if Johnny measures a distance on his original of 4 and 7/16 inches, he simply looks at the dial to find that he needs to mark off about 5 and 3/4 inches on the scaled reproduction. And, since the scale is circular, all necessary proportions for future measurements are available at once.
8.10.3 Special Chemistry
Speaking of proportions, the concept is especially useful in certain calculations performed in the study of chemistry, wherein chemical compounds can only be broken down into specific ratios of component compounds or elements, due to the integer nature of the periodic table. Due to this fact, and since logarithmic scales lend themselves directly to finding ratios, scales on slide rules that were calibrated with the molecular weights of elements and compounds were created in the early 1900s. For example, the Chemiker Model 33 slide rule was introduced by Nestler in about 1912. The one in the Collection, from between 1928-1933, is shown here:

For example, suppose we have a sample of lead chromate, whose chemical symbol is PbCrO\(_4\), that weighs 5.4 grams. What is the total weight of lead (Pb) in the sample? On the chemist’s slide rule, we find the markings for the molecular weight of lead and for the molecular weight of lead chromate and line them up using the cursor:

On this slide rule we find Pb on the stock, and PbCrO\(_4\) on the slide. Our ratio has now been set. So, by looking at the C and D scales on the rule, we find the value 5.4 on the slide (where PbCrO\(_4\) is found) and opposite this on the stock is the corresponding number for Pb – approximately 3.46. So, the sample would have 3.46 grams of lead. And, voila, we have performed our chemistry calculation on our specialty slide rule. OK, you might ask how do we know the answer isn’t 0.346 grams, since we cannot differentiate factors of ten on the C and D scales? Well, that’s why we need people who get degrees in chemistry (and why it was a specialty slide rule made for just such people).
There was a variety of chemistry slide rules, from K&E and Hemmi for instance. We have a Hemmi 257 in the Collection, which is shown below. It is a duplex slide rule with a standard scale arrangement on one side, and the “chemistry” scales on the other (shown in the figure). In addition to the standard proportions, it can also be used to do temperature conversions and other computations related to ideal gases and their pressure variations.

It is sometimes hard for some to think of a proportions scale as a “specialty” slide rule – it is, after all, just a standard set of logarithmic scales found on any standard slide rule. However, the people using them weren’t always scientists and engineers. They were often times people in various business settings, the industrial trades, the arts, and so on, and they just needed to get the numbers right and get on with their work. These special slide rules were generally produced with scale ranges that were tailored for their everyday use and allowed users to do their jobs much more efficiently and effectively. This is why simple proportions scales were so prevalent and why they can still be found for sale today.
