8.24 Scale Wars
The turn of the 19th century into the 20th was a period of significant fluctuation in the design of slide rules and their scales. Not only was the mechanical structure of slide rules rapidly developing during this period, with celluloid laminations and adjustment screws and self-adjusting mechanisms, but there appears to have been a significant amount of investigations into various scale layouts as well. In particular, I would like to contrast and compare what was going on in the U.S. companies Keuffel and Esser, Eugene Dietzgen, and Kolsech at this time as good examples of the slide rule development trajectory.
To start, we first recognize that the Manheimm layout of the standard A, B, C, and D scales was patented in France by Amédée Manheimm in 1850, followed by his patent of the modern “cursor” in 1851. As briefly discussed in Comments on Scale Development, the Manheimm layout was a relatively slight adjustment to the Engineer’s rule scale set, which itself was a slight adjustment to the Carpenter’s rule scale set. For almost 50 years no new ground-breaking feature was introduced to the slide rule layout. While the Carpenter’s and Engineer’s rules also had scales labeled “A, B, C, and D”, it was the Mannheim rule and its popularity that enshrined these labels with their modern-day meanings: logarithmic scales of two decades (A/B) or one decade (D/C) on the stock/slide of the rule. Meanwhile the use of all of these instruments continued to grow throughout Europe and America. And in America, only Gunter, Carpenter’s, and Engineer’s rules were being made by a few companies, while most slide rules, including Mannheims, were being imported from Europe.
8.24.1 Thacher and Scofield
A couple of important scale developments occurred in the late 1880s and early 1890s by two engineers working on the design and construction of some of the large bridges across some of America’s major rivers, and this is where we begin our story. Edwin Thacher introduced his patented Calculating Instrument in 1881 (U.S. Patent No. 249,117), with production of the instrument almost immediately being taken over by Keuffel & Esser as their first in-house manufactured slide rule. Most people quickly understand the implications of having an 18-in long instrument with the computing power of a 30-foot slide rule to get more accuracy in their results. However, the Thacher slide rule had another very important feature which is often times overlooked.
Thacher realized that when using a slide rule, it is often the case that the result one is looking for is “off scale”, which requires the slide rule index to be reset. This might not be too much of a bother when using a 10-inch Mannheim rule, but when carefully aligning two 4-digit numbers on a Calculating Instrument, one may not like going through the process again after having access denied to the results one is seeking. Also, in engineering applications, it is often the case that the user wants to explore a range of possible values to use in a design, for instance. One might have a problem such as
\[ x =\frac{A\times c}{B} \]
where perhaps we seek a value for \(x\), given constants \(A\) and \(B\), but \(c\) is, say, “flexible” in what values we can use in our design. In such circumstances, one might set up the problem in terms of ratios:
\[ \frac{x}{c} = \frac{A}{B}. \]
The ratio \(A/B\) can be set on a slide rule and then, immediately, all possible ratios of \(x/c\) can be seen at once and an appropriate set can be chosen by the designer.
Of course not all ratios can be seen at once, if many of them are “off scale”! So this was the other issue that Thacher solved with his Calculating Instrument design. He added a second, complete dual set of logarithmic scales onto the calculator, where this new set of scales had an offset from the original set of scales. The offset was half the length of the instrument. This meant that if the inner cylinder of his Calculating Instrument was extended such that results were “off scale” for his main scales, then these results would be accessible on the second set of scales. With one setting of a ratio on the main scale, all combinations of other numbers giving that ratio could be seen at once. A scale with an appropriate offset as described above would soon be called a “folded scale”.
Now in 1889, Thacher hired an assistant, bridge engineer Edson Mason Scofield. Within two years Scofield, who also had a knack for computations as did Thacher, had created a prototype of a new slide rule that he was calling the “Three Multiple Slide Rule.” Again, accuracy in engineering results was the key issue being addressed. Some of the bridges being built across the Ohio river, for instance, were up to a mile long and extremely costly. First of all, the slide rule had logarithmic scales that were roughly 20 inches in length or more. And secondly, since every time the slide was set on the rule some amount of inaccuracy would be introduced, his slide rule could be used to multiply three factors with only one setting of the slide by using an inverse scale. A prototype of Scofield’s slide rule was documented in 1994.89
The Three Multiple Slide Rule never went into production. It also had the typical problem of often finding solutions to be off-scale. But by 1901 Thacher and Scofield had come up with a new slide rule scale layout, which was dubbed The Engineer’s Slide Rule, that was patented in that year (No. 677,817). Taking concepts from both the Calculating Instrument and the Three Multiple slide rule, the Engineer’s Rule had scales on both sides, with separate slides on each side. The front had scales with reciprocals and square roots for performing a wide range of “ratio” calculations, while the back had full-length “D and C”-type scales on the top and “CF and DF”-type scales on the bottom, where the folds were at \(\sqrt{10}.\)
Below is an image of the slide rule set to multiply three numbers: 1.6 times 7.8 times 3.7. To perform the calculation, we put 7.8 on the slide opposite 1.6 on the bottom scale. Since the bottom scale is a reversed scale, this amounts to a multiplication. Hence, the intermediate result is at the index of the bottom scale. But this is at the same location as the index of the upper scale. So, finding 3.7 on the upper scale, we find the result – a tad less than 46.2 – on the slide.
When needing to find a solution to a certain ratio, the other side of the rule allows for all ratio values to be visible at once, with the accuracy of a 22-inch log scale.
Very soon after the slide rule was produced in 1901, Dietzgen became the sole distributor of the rule, and it was available from their catalog from around 1901 until at least 1931.
8.24.2 The Duplex
But at the time of the early development of Scofield’s slide rule, another very important development occurred. In 1891 William Cox, of England, patented his concept of a “duplex” (double-sided) slide rule while working as a mathematical consultant to K&E in the U.S.90 This revolutionary step in the slide rule story simultaneously connects any number of scales on the front and back of a double-faced slide rule. Cox assigned his patent (No. 460,930) to K&E, as K&E was becoming the first major slide rule manufacturer in the U.S. Their production line soon included Thacher’s Calculating Instrument, standard Mannheim rules, as well as the new Duplex slide rule. And as the U.S. patent has a 17-year period, it was quite awhile before another manufacturer could produce a double-sided duplex rule of this nature to compete with K&E. The first Duplex rules hit the market in about 1895.
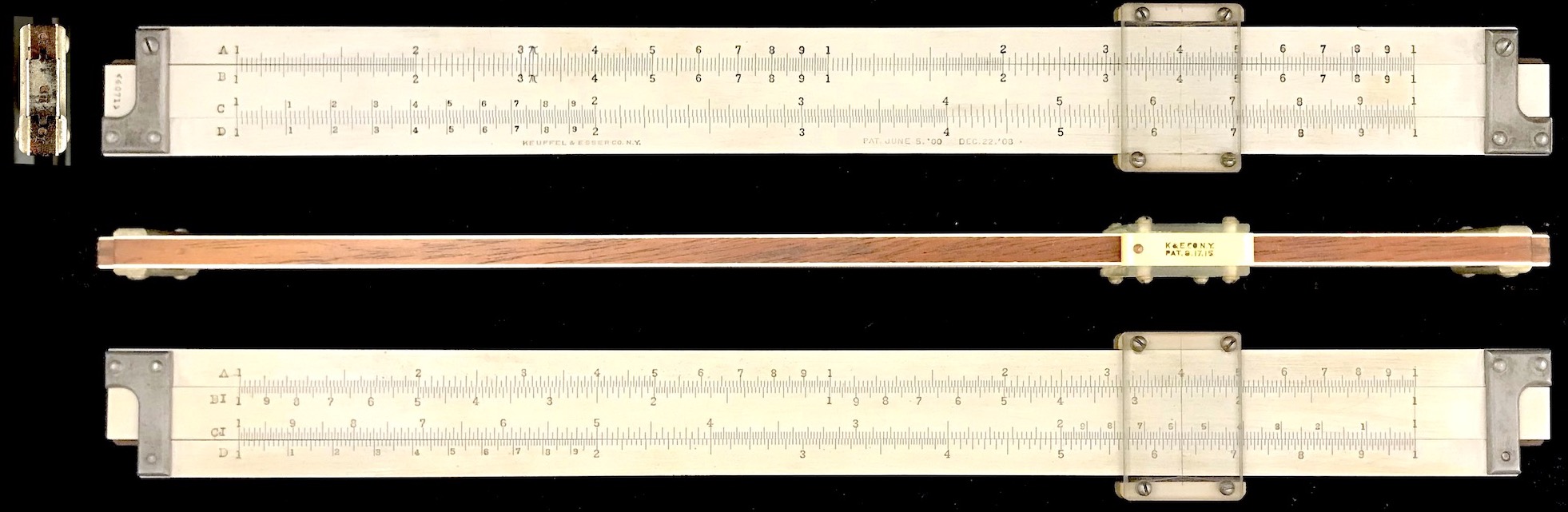
As is common in such steps forward, the Duplex rule allowed a person familiar with the standard Mannheim to continue using the front face of the Duplex as before. But now, extra scales could be added to the back of the rule that are also connected to those on the front. The first application was to add reversed, or inverted, scales on the back that could be used for additional multiplication and division of numbers with only one setting of the slide. It is not known what role Scofield or Thacher may have played in making this choice, if any, but clearly the ability to multiply or divide three numbers with one setting was an attractive option for the first use of the Duplex design.
For a numerical example in using the Duplex, suppose we again want to multiply 1.6 times 7.8 times 3.7. We can set the 1.6 on the CI scale against the 7.8 on the D scale on the back of the rule. (See cursor in the top image below.) Simply turning the rule over, we can locate 3.7 on the C scale using the cursor. (See bottom image below.) The number below on the D scale is the product of the three: about 46.2.
Through the use of the Duplex, multi-numeric operations could be performed not only more quickly, but also with less error in the result due to the limited times that the slide would need to be reset. This gave K&E’s new double-sided mahogany slide rules a great selling point and helped to quickly put them on the map world-wide.
K&E’s patent language was very well written and strong enough to keep any other manufacturers from introducing a slide rule with the front and back connected through a cursor. It meant that competitors had to find other ways to perform operations with three numbers on a single setting.
Though the Scofield Three Multiple rule was prototyped in 1891, the Engineer’s Slide Rule of Thacher and Scofield was not patented until 1901, a few years after the first Duplexes. Interestingly, K&E very quickly introduced a very high-priced Duplex rule in 1901 that included features from Scofield-Thacher. Their Universal Slide Rule, Model 4090, in addition to the usual scales of the Mannheim, included reversed A, B, C, and D scales, a folded logarithmic scale set, and a folded inverse scale set. The folds were at \(\sqrt{10}.\) It sold for $20 that year, compared to the $5 Scofield Engineer’s Slide Rule offered by Dietzgen. It was last seen in the K&E 1911 catalog.
8.24.3 The Multiplex
In the meantime, things were brewing just 800 miles to the West. We’ve mentioned Dietzgen a few times already. Eugene Dietzgen, an ex-K&E employee, was creating his own slide rule manufacturing operation in Chicago, Illinois during this period. In the early 1880s Dietzgen started his business career as a Midwest Representative of K&E based in their local headquarters in Chicago. Remember that K&E was not manufacturing their own slide rules yet. Dietzgen eventually teamed up with a manager of the A.H. Abbot & Co.’s mathematical and drawing instruments department, Otto Luhring, to form the company Luhring & Dietzgen in 1885. In 1891 Dietzgen bought out Luhring’s shares and started Eugene Dietzgen and Company. By 1893 Dietzgen opened his own manufacturing plant to produce T-squares, drawing boards, surveying equipment, and other relevant supplies and the company was renamed the Eugene Dietzgen Company.
Then, in 1898 Dietzgen acquired a U.S. patent (No. 606,388) that was granted to John Givan Davis Mack in that year (the “Mack Improved Mannheim Simplex Slide Rule”). Mack was a professor of engineering at the University of Wisconsin in Madison.91 The Mack Improved slide rules, which have pins and springs embedded in the slide rule to maintain alignment, were a successful improvement to the general slide rule design and were sold from 1902 to 1912, giving Dietzgen national attention. While Dietzgen is noted as a major slide rule maker, they bought their parts mostly from German sources and performed final assembly of their rules in Chicago. K&E, on the other hand, started out that way, but by now was making their own slide rules completely “in house”. It was not unusual for Dietzgen to obtain rights to sell slide rules made by others, the Scofield-Thacher Engineer’s rule being a case in point. Future similar arrangements would arise with companies such as Richardson, Gilson, and others.
Now during this period, in 1904, Leon Walter Rosenthal of New York City was granted a patent for a scale arrangement with a special scale on the slide. On most slide rules the “B” scale runs from 1 to 10 to 100, or two decades, from left to right. On Rosenthal’s B scale, the numbers run, left to right, from 10 down to 1 and back up to 10 again. From his knowledge and experience with the Scofield rule, and not being able to produce a Duplex rule, Dietzgen no doubt recognized the significance of this new concept. The Rosenthal patent (No. 767,170) was acquired by Dietzgen that year and was immediately applied to their slide rule repertoire with a new model, the 1762. While the K&E Duplex rule provided a new method for multiplying or dividing three numbers with one setting, the rule was also quite expensive. The Rosenthal simplex design provided the same function but without having to turn the rule over. One could argue that the decade of a B scale is half the length of a C or D scale, and hence not as accurate. While this might be true, for those not requiring that level of improved accuracy the same function can be acquired with the rule lying on the table. The new model could be produced through a simple scale change on an otherwise standard Dietzgen slide rule, and thus provide three-factor capability on one of their quality products.
Below is an image of a Rosenthal rule with its special “B” scale. Its distinctive feature is how the numbering emanates from the center of the B scale, increasing to the left and to the right from the central “1”. To distinguish the two parts of the B scale, the left-side of B is called the Br scale (“r” for reversed, or perhaps for “Rosenthal”, or perhaps for both), and the right-side of the B is called the B’’ scale. (For comparison, in the Dietzgen literature the standard A and B scales are often treated as having two parts, the A’ and A’’ scales, and the B’ and B’’ scales, each designation referring to a left or right “decade”.) But note that the scale is simply labeled “B”, just like any other Mannheim rule. One needs to look closely at the numbering to see the difference. Dietzgen dubbed their rule the “Multiplex Slide Rule” and variants of this model were available from 1905 until about 1926.
For comparison, let’s perform our earlier calculation using the Dietzgen rule. The operation is illustrated in the image below. Since dividing by a reciprocal is the same as multiplying, we can line up 1.6 on A’ with 7.8 on Br to perform the first multiplication. The result would be on the A scale at the central index of the B scale. (In our case, 12.5.) Then, simply finding 3.7 on B’’ multiplies this first result and gives the final result on A’’: about 46.2.
8.24.4 The Triplex
But Dietzgen wasn’t the only one looking to compete with the new Duplex rules. At about the same time, another company, New York’s Kolesch & Co., was also getting involved in this pursuit.
During the turn of the century, Dennert & Pape and Nestler were the world leaders in slide rule production. Working together, much of the stock used to make their rules was being produced by D&P, and Nestler had the world’s best engine dividing machines used to engrave the stock with highly precise scales. The tooling of their dividing engines could be changed fairly rapidly, yielding fast turn-around times and the ability to produce small batches of rules for outside customers. A discussion of a Nestler prototype for Dietzgen of a Rosenthal slide rule is described in the vignette, Dietzgen Rosenthal Nestler Prototype. And both Dietzgen and Kolesch sold slide rules with their respective names on them, but which were obviously produced by Nestler.
One of the slide rules sold by Kolesch, called the “Triplex”, was introduced in about 1907. Like Dietzgen’s Multiplex, the Triplex (which does not appear to have been patented) used an inverse scale to set up a three-factor multiplication problem with one setting. However, this reversed scale was a single-decade scale of similar length of the C and D scales and hence did not give up on accuracy, much along the lines of Scofield’s prototype.
Whereas the Multiplex has the “Br” scale as part of the B scale arrangement, the scale set of the Triplex is simply a different take on traditional scales. In terms of modern scale labels, it goes like this:
A D [ CI C ] D K
Once again let’s perform our earlier calculation using the Triplex rule, which is illustrated in the image below. We line up 1.6 on D (upper) with 7.8 on CI to perform the first multiplication. The result would be on the D scale at the index of the CI scale, which is also the index of the C scale. Hence, we are in position to perform the next multiplication by finding 3.7 on C, below which we find the final result on D (lower): about 46.2.
The Triplex discussion in the first edition of Kolesch’s book, How to Use Slide Rules,92 emphasizes the use of the “additional triple scale” which today would be called the K scale. This may be how the slide rule got its name, though just four paragraphs later 3-factor multiplication is also described:
The arrangement of the four middle single scales also permits the multiplication of three numbers in one setting. Thus, for instance, to multiply 2x3x6 set 2 on inverted scale under 3 on adjoining rule scale and read 36, the result, on D scale under 6 on C scale.
In like manner the arrangement often conveniently permits consecutive division with one setting.
8.24.5 The Duplex Redux
Naturally, Keuffel and Esser did not sit still, but rather continued to give their Duplex slide rules ever more powerful functionality. Besides the basic Duplex rule introduced in the late 1800s, they introduced their new Log-Log Duplex rule – the 4092 – in 1909. The 4092 had the standard A,B,C, and D scales on the front but, along with the new log-log scales, it had CI, C, and D scales on the back of the rule. This allowed for three-factor multiplications and divisions in much the same way as with the Triplex.
Now when multiplying three numbers together, the order of the multiplication can typically be chosen so as to not have the answer fall off-scale. For example, if we multiply three numbers between 1 and 10, we put the smallest number on D, say, and the largest number on CI, and then the middle number is more likely to be available on C, with the answer on D. However this often is not the case, and when extended to further multiplication of more factors it can become harder to avoid having results that fall off-scale, in which case the user must “reset” the index, or perhaps start the calculation all over again. Such a scenario could be overcome largely by the introduction of a “folded” scale. With an offset that is half the length of the standard scale (i.e., physical length, not numerical length), then if a number being sought is off-scale, it should be available on the folded scale. As previously noted, such a solution to the “off-scale” problem was introduced by K&E in their Thacher’s Calculating Instrument, which uses two standard logarithmic scales offset from each other. The same solution to this problem was introduced by K&E in 1913 with their new Polyphase Duplex rule, the 4088, which included scales DF,CF,CIF,C, and D on the front and CI and D scales on the back.
The “fold” of the CF, DF, and CIF scales is at \(\pi\). K&E realized that having the fold at a value of \(\pi\) = 3.142, rather than \(\sqrt{10}\) = 3.162, would accomplish the same goal in almost all circumstances, but would provide a scale that could be convenient in other calculations as well. Interestingly, Thacher and Scofield knew this, too. Thacher patented a folded scale concept in 1902 (No. 701,103), with the patent half-assigned to Scofield, seemingly in anticipation of this impending development. (See The Scofield Engineer’s Slide Rule.)
The Model 4088 scale arrangement with combinations of folded and inverted scales allowed for even more factors to be multiplied with a minimum number of re-settings of the slide. The 4088 also eventually came in four different scale lengths of 5, 8, 10, and 20 inches. (See The Long and Short of It.)
8.24.6 The Dietzgen Phillips
Not to be left behind, Dietzgen continued to play with alternate scale layouts for awhile. In 1919 they introduced their Phillips Slide Rule – Model 1759 – which included an inverse B scale which they called the R scale. (Later, a more standard name for such a scale would become BI – inverted B scale.) William Oliver Phillips, of Riverside, Illinois, received a patent (No. 1,088,175) in 1914 for slide rules with certain reversed scales, though the patent does not appear on the Dietzgen slide rules. An example of the Dietzgen Model 1759-B is shown in the image below.
From the Dietzgen catalog,
The reciprocal scale “R” is an inverted, double logarithmic scale of the same unit length as the “A-B” scales to which it is referred. This scale permits rapid reading of divisions and inverse proportions, and enables three factors, such as 97 x 98 x 99, to be taken without resetting the slide. It is an unique scale found only on the Phillips rule.
The Phillips eventually came in 8, 10, and 20 inch lengths. It also continued to perform main calculations using the A/B and R scales, rather than using C/D.
8.24.7 The Duplex Redux Part Deux
But then, in 1922, K&E revamped its Log-Log rule into the 4092-3 and 4092-5 (10- and 20-inch versions). The new scale layouts included the powerful DF [ CF CIF CI C ] D arrangement from the 4088. So in addition to having the Log-Log scales on the back side, this slide rule also facilitated the multiplication of any five factors with only two settings of the slide.
As an example of the use of the 4088/4092 scale set, let’s take the product 6.3 x 2.5 x 0.17 x 9.3 x 2.8. Consider aligning 6.3 on D with 2.5 on CI. (See circled region in image below.) The intermediate result would be at the index of CI, which is also the index of C. So, moving the cursor to 0.17 on C gives the next intermediate result below on D (2.68). We can now re-adjust the slide to align 9.3 of CIF with the cursor. (See red line in lower image below.) Next, moving the cursor to 2.8 on CF the result will be under the cursor, on D: 69.7.
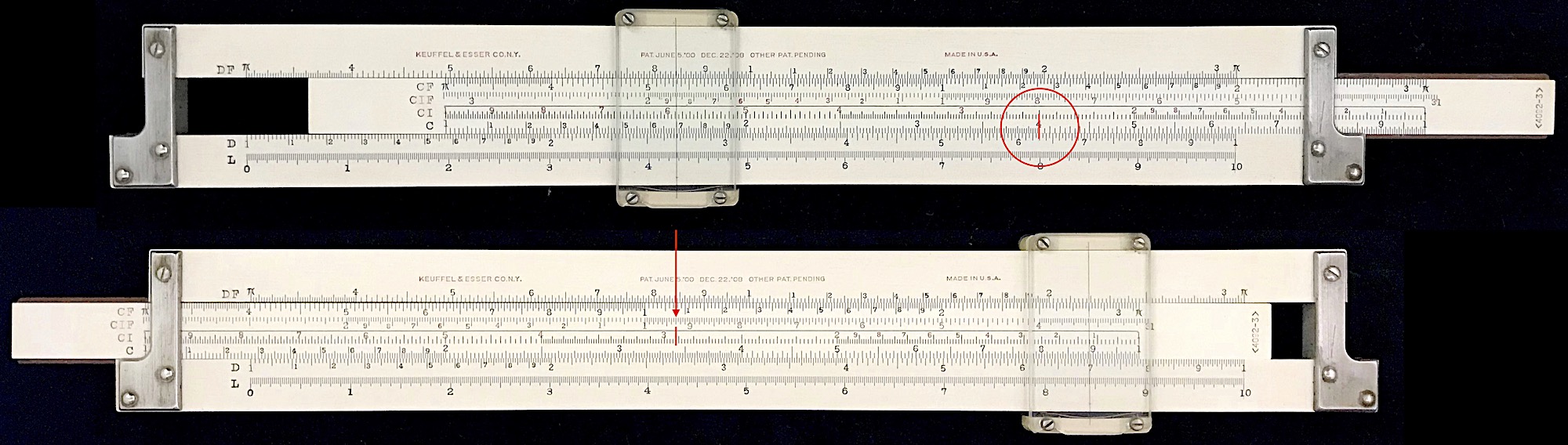
The 4092-3 and 4092-5 (20-inch version) in 1922 were perhaps the most powerful slide rules yet. They could multiply five numbers with two settings, could take arbitrary numbers to arbitrary powers, find natural logarithms and exponentials, and of course included log, sine, and tangent scales as well. Within a year or so a K scale was added, and the 4092 family went on to be sold through 1938.
8.24.8 The Calculex
As the above series of events was transpiring in the US, J. Halden & Co., Ltd. of Manchester, England, was designing and selling drawing and surveying instruments. Their popular “Calculex” slide rule, a circular pocket-watch style slide rule that was introduced by Halden in about 1906,93 was also apparently participating in the Scale Wars. The Calculex has a reversed scale on its back side and so has the capability to perform three-factor multiplication with one setting. (See image below.) In its instruction book, under the topic of “Multiplication”, it states,
If there are three factors to multiply, … On reverse scale, set the first factor on A to second on B. Turn over to front face and read result on B opposite third factor on A.
To perform our previous example, on the back side set 1.6 on A against 7.8 on B (reversed scale); on the front, find the result 46.2 on B opposite of 3.7 on A. Clean and simple.
To round out the discussion, note that in Germany, the Rietz scale arrangement (DRGM 181 110) had been established in 1902. This was an important innovation and historic step in the standardization of scales and scale arrangements. However, Dennert and Pape did not add an inverse scale to their “System Rietz” until 1926.94 Nestler, on the other hand, deployed their Model 34 with a reciprocal scale in 1911, though it was a specialty rule with low production numbers.95 The Nestler catalog of 1911/1912 describes this model, with design features for electrical engineers, as allowing for multi-factor multiplication. By 1914 Nestler was selling models for which inverse scales could be added to the slide rule at additional cost. From the 1914 catalog:96
Several Nestler models began having reciprocal scales as part of their standard arrangement by the early 1920s.
Back in the U.S., The Frederick Post Company, also of Chicago, was selling German-made rules. Their Model 1452 – the Mannheim Multiphase Adjustable 10” Slide Rule – included a CI scale and was introduced in 1925. From the Post catalog (1925, 1927, and 1930),97
The inverted scale of the Multiphase Rule permits performing multiplication and division, or both, with three numbers in one setting.
Post also introduced a duplex rule in 1925, the Model 1458 – Multiphase Duplex Slide Rule – which included CI on the front and DF, CF, and CIF on the back. These rules were produced by KHH. Though popular in America, the duplex slide rule was not as popular in Europe and did not begin to catch on there until the mid-1930s.98 It was also about 1930 when Hemmi began manufacturing rules with CI scales as well as duplex slide rules, at about the time when they started producing the Model 1458 for Post. Interestingly, Dietzgen did not produce its first duplex slide rule until the 1940s, while Kolesch – to my knowledge – never sold a duplex rule, certainly not one with their name on it.
8.24.9 The Winner
In the end, it appears that K&E won the Scale Wars of the early 1900s. Their early Duplex rule was a natural extension of the Mannheim, and users didn’t need to learn how to use a new split-B scale (nor make mistakes by thinking it was a standard B scale). Guarded by their strong patent, by the time competitors came up with new simplex designs K&E was beginning to introduce even more powerful duplex slide rules that included multi-factor-friendly scales. Even the popular Versalog slide rule, introduced by Post in 1951, used the 1913 DF [ CF CIF CI C ] D arrangement of K&E on its front side. As a matter of fact, the present slide rule collection has 44 slide rule models made by 12 different makers that have this exact scale arrangement. And the duplex slide rule – eventually found on a multitude of makers’ platforms – continued to adorn the most advanced slide rules until the end of the slide rule era, some 90 years after its introduction.
As for the original Scofield-Thacher Engineer’s Rule, somehow this rule did not gain popularity among users. Perhaps this was due to its inferior construction. So even though it was very early on our time scale and, in fact, was available throughout most of the period we are discussing, it never had the appeal or sales of the other competing models. I like the theory that Dietzgen bought the rights to sell the slide rule, which may have been produced en masse by Scofield in 1901 after receiving a patent. And, after all, Thacher and Scofield were in the business of building bridges, not slide rules. Who knows, perhaps Thacher and Scofield had the last laugh, with their early patents for their folded and reversed scale layouts.
All of that being said, I want to reiterate that the 1906 Calculex was a very interesting and competitive option for the multi-factor multiplication application. Its two-sided pocket-watch-style design is essentially a duplex and, being circular, it does not have the need for “folded” scales, making its operation all that much simpler. And it fits in one’s pocket to boot!
Scale Wars Timeline
| 1881 | Thacher applies for, awarded patent, Calculating Instrument |
| 1889 | Thacher hires Scofield |
| 1891 | Scofield prototypes “Three Multiple Slide Rule” |
| 1891 | Thacher moves to New York |
| 1891 | K&E purchases rights, begins producing Thacher’s Calculating Instrument |
| 1891 | Cox applies for, awarded patent, duplex concept; assigns to K&E |
| 1891 | Eugene Dietzgen Company formed |
| 1895 | K&E Duplex rule (1744) introduced |
| 1899 | K&E re-numbers models, 1744 \(\rightarrow\) 4070, etc. |
| 1900 | Thacher and Scofield apply for patent, Engineer’s Rule |
| 1901 | Thacher and Scofield awarded patent, Engineer’s Rule |
| 1901 | Dietzgen begins sale of Engineer’s Rule |
| 1901 | K&E 4090 Universal Duplex introduced |
| 1902 | Thacher and Scofield apply for, awarded patent, regarding folded scales |
| 1903 | Scofield forms Scofield Engineering Construction Company in Philadelphia |
| 1904 | Rosenthal applied for, awarded patent, Br-B’’ scales |
| 1904 | Dietzgen Multiplex (Rosenthal) introduced |
| 1906 | Halden Calculex introduced |
| 1907 | Kolesch Triplex introduced |
| 1909 | K&E 4092 Log-Log Duplex introduced |
| 1912 | Phillips applies for patent, R scale (reversed B) |
| 1913 | K&E 4088 Polyphase Duplex introduced |
| 1914 | Phillips awarded patent, R scale (reversed B) |
| 1914 | Nestler offers inverse scales for additional cost |
| 1919 | Dietzgen Phillips Rule introduced |
| 1922 | K&E 4092-3,-5 Log-Log (Polyphase) Duplex introduced |
| 1925 | Post introduces 1452, 1458 (duplex) with inverse and folded scales |
From Mike Frey’s magnificent K&E Timeline, the first Duplex rules were offered in 1895, with a larger proliferation of Duplexes being sold beginning in 1901. A Dietzgen time line has been documented by Bruce Babcock, wherein we find that the first iteration of the Multiplex rule was sold by Dietzgen in 1905, with the second iteration available in about 1910. The Kolesch Triplex, from their catalog and book, was offered beginning in 1907-1908. And the early Phillips rules were introduced in about 1919. In Germany, though Nestler, KHH, and D&P helped produce the new US slide rules, they did not include reversed scales on their own rules until the newer versions of the Rietz layout in about 1911 (Nestler) and 1926 (D&P).99 Some history of the early Calculex can be found in an article by Peter Hopp.100
Note that much of this article has been compiled from information first written in the vignettes entitled Dietzgen Rosenthal Nestler Prototype, Carpenters vs. Engineers, The Scofield Engineer’s Slide Rule, and Rule Change 4092-3, as well as information found at other locations within the web site.
Conrad Schure, “The Scofield-Thacher Slide Rule”, Jour. Oughtred Soc., 3.1 p20 (1994).↩︎
See articles Jour. Oughtred Society 10.1 p29 and 13.2 p20.↩︎
D. Petri-Palmedo, How to Use Slide Rules, Kolesch & Company, New York, 1908.↩︎
Florian Cajori, A History of the Logarithmic Slide Rule and Allied Instruments, The Engineering News Publishing Company, New York, p102 (1909).↩︎
Hans Dennert, “DENNERT & PAPE and ARISTO Slide Rules 1872 – 1978”, Jour. Oughtred Soc. 6.1 p5 (1997).↩︎
Andreas Faßbender, private communication.↩︎
Ibid.↩︎
See https://sliderulemuseum.com/srtco/PostCrossRef/SubPages/1452%5b1925-30%5d.html.↩︎
See Dieter von Jezierski, “The Duplex Slide Rules of Faber-Castell”, Jour. Oughtred Soc. 17.2 p17 (2008). ↩︎
See “Slide Rules of the Major Makers” on the Oughtred Society web site.↩︎
Jour. Oughtred Soc. 8.2 p 45 (1999).↩︎