8.32 Gauging and Excise Tax Slide Rules

The first slide rules were simple logarithmic scales that could be slid back and forth to perform quick multiplication and division problems with few-digit accuracy. Within just a few decades, people began to find special uses for “sliding rules” other than rudimentary astronomical and navigational calculations, but rather for more practical everyday uses in business, government, and civil engineering. And what would be more useful than a slide rule for figuring out how much tax to charge someone for the alcohol content in their wine or whisky barrels?

The definition of “gauging” (or gaging; from the Old French word jaugier) in our context is “to measure precisely the size, dimensions, or other measurable quantity of; to determine the capacity or contents of.”125 So imagine a wine maker rolling out a cask of wine and a tax excise officer wanting to know the number of gallons of liquid in the cask, and wanting to know what fraction of that liquid is actually alcohol. After making a few measurements of some vital dimensions, the officer can use a special slide rule to calculate the number of gallons being held in the barrel. The gauging slide rule was one of the very earliest types of specialty slide rules that came into widespread use in late-1600s England after the slide rule’s invention earlier that century.

8.32.1 Gauging the Contents of a Barrel

Barrels or casks come in a variety of shapes and sizes and so the job of the Gauger was to determine the interior volume of the barrel and, more importantly, the volume of liquid contained therein. The simplest barrel configuration to consider could be that of a cylinder. The volume of a cylinder is nothing more than the area of its circular base multiplied by the length of the cylinder, \(V = \pi R^2 L = \frac{\pi}{4} D^2 L\), where \(R\) is the radius, \(D=2R\) is the diameter, and \(L\) is the length of the cylinder along its axis. A beer, wine, or whisky barrel, however, is formed so as to bulge at the middle of its axis, allowing for much easier transport of the barrel by rolling. (See figure below.) As cork or rubber stoppers, or “bungs”, were typically located at this bulge location for accessing the liquid inside, the term bung diameter, \(B\), is often used to describe this largest middle dimension.


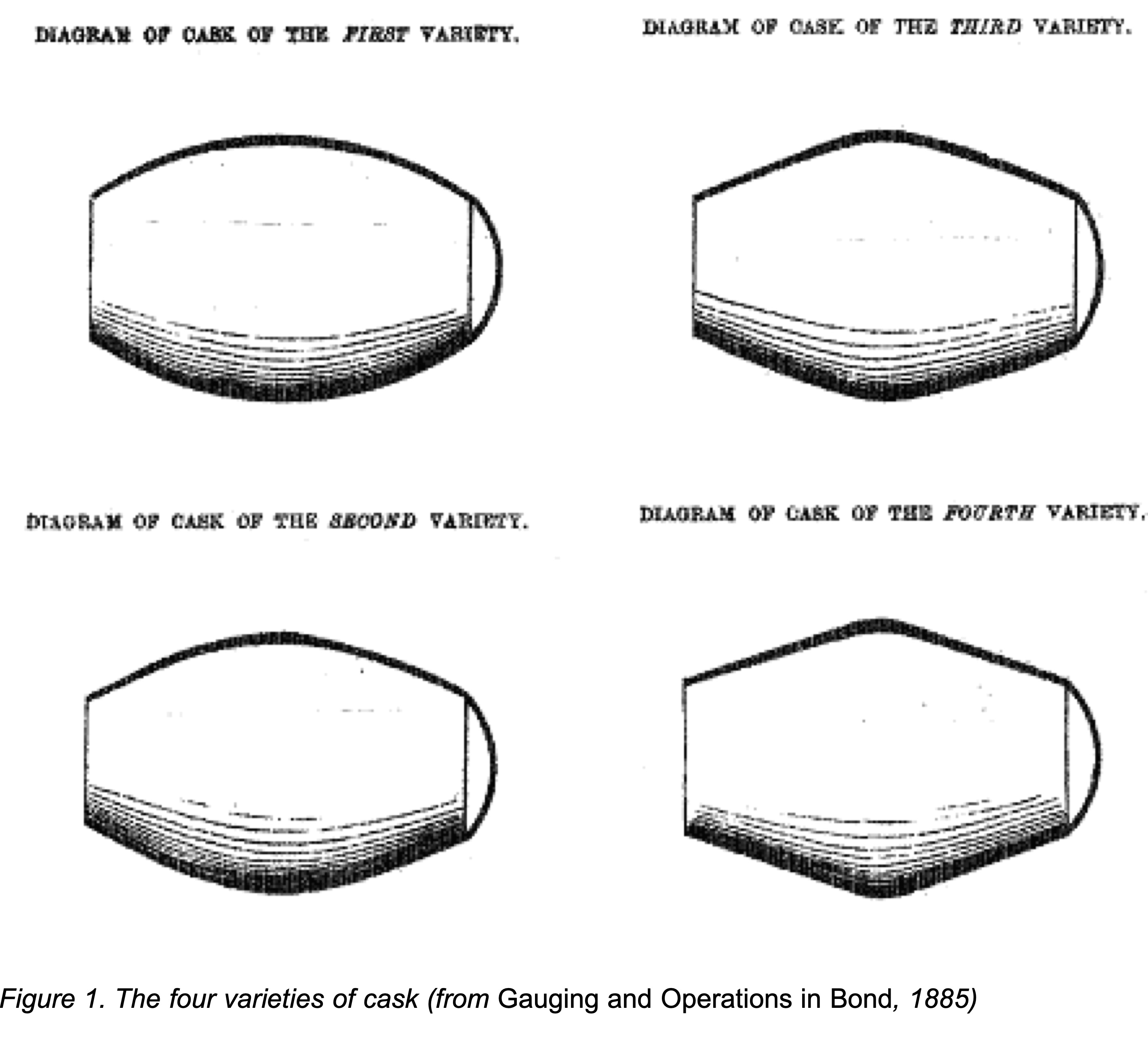Four standard barrel types in the 1800s


The right-hand image above, taken from The Excise Officer’s Manual of 1840,126 illustrates a variety of cask shapes found in the middle 1800s. The first variety is a simple spheroidal barrel with elliptical cross-section. This is a very natural shape, but as casks were built and tensions put on the planks of wood, often the casks would acquire various distortions which were characterized by the other varieties. For our purposes of our present discussion, let’s concentrate on a model of a spheroidal cask as depicted here:

To compute the volume of such a barrel with its truncated flat ends, we remember that the general equation of an ellipse is

\[ \left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = 1 \]

where the elliptical cross section of the barrel has semi-major and semi-minor axes of lengths \(a\) and \(b.\) At \(x=0\) we would have \(y=B/2.\) At the two ends of the barrel its diameter is \(H\), also called the head diameter, and so we have \(y = \pm H/2\) at the locations where \(x = \pm L/2.\)

If the region inside the barrel is divided up into fine segments each of length \(\Delta x\) along the long axis, then each of these thin discs (one of which is depicted in light blue, above) along values of \(x\) can be thought of as its own cylinder and its individual volume would be \(\pi y^2 \Delta x\), where \(y\) is the distance to the inside of the barrel from the \(x\)-axis: \(y = \frac{B}{2}\sqrt{1-(x/a)^2}\). Summing up all of these volumes starting at \(x\) = 0 and ending at \(x=L/2\) would give an approximation of the volume of half the barrel. Multiply by 2 and you have the total volume. The remaining quantity in our description above is the semi-major axis, \(a.\) But this can be determined from our other defined parameters. For a spheroidal barrel described above, we find that

\[ a = \frac{L}{2}\cdot\frac{1}{\sqrt{1-(H/B)^2}}. \]

The summation of our thin segments can be calculated directly using calculus and the volume of the cask is found to be:

\[ V ~~ = ~~ \frac{\pi}{4} B^2 L\cdot \left[ 1 - \frac{1}{12}\left(\frac{L}{a}\right)^2\right] ~~~~ = ~~~~ \frac{\pi}{4} B^2 L \cdot \left[ \frac23 + \frac13\left(\frac{H}{B}\right)^2\right]. \]

As can be seen, the factor in front of the brackets in the equations above yield the volume of a cylinder of diameter \(B\) and length \(L\), while the bracketed quantity itself gives the reduction of this volume due to the curvature of the true spheroidal barrel or cask. Note that as \(H\) goes to zero in the equation above we get the volume of a complete spheroid as we should: \(V_{sphd} = \pi/6\cdot B^2L\).

8.32.2 Volume Calculation Examples

A computer code:

B = 32
H = 24
L = 40
in3Gal = 277.274
Vgal = pi/4*B^2*L*( 2/3 + (1/3)*(H/B)^2 )/in3Gal
Vgal
## [1] 99.1022

The amount of effort required in the gauging of wine and whisky barrels in the early slide rule days was reduced by (a) creating a standard set of barrel shapes to model the barrels being used in the industry, and (b) creating slide rules with scales that could be used to get good approximate answers quickly and efficiently. As an example, consider again our first-variety barrel or cask that has an elliptical shape to it. Let’s assume we have a cask with \(B\) = 32 inches, \(H\) = 24 inches, and a length \(L\) = 40 inches. Note that in the mid-1800s England the Imperial Gallon was equivalent to 277.274 cubic inches.

From our formula above we find \(H/B\) = 0.75 and \(V\) = 99 gallons using a computer. We now perform the calculation on a gauging slide rule.


The gauging rule we will consider is a Dring and Fage rule from c. 1845, London, shown in the figure below. This particular slide rule is roughly 10 inches in length, is double-sided, and has two separate slides to be used in calculations. It has a total of 26 separate scales, not including a standard inch scale on one edge. It also has a number of stains on it, indicating that it was heavily used in its day.



The scales on the slide rule can be used for standard multiplication and division calculations, and squares and square roots. It then has special scales to be used to determine the volumes of casks of four major varieties, including that of the spheroid, and for determining the volume of liquid inside of the cask based upon rod wet/dry measurements. While some scales are labeled A, B, C, and D, they do not necessarily represent the more modern slide rule scales with these names. Let’s use this rule to perform a couple of calculations…


  • Volume of a Cylinder

The major scales of interest for this calculation are the C and D scales. The C scale is a 1-decade-long logarithmic scale, located on the upper slide on one side of the rule. The D scale, located on the stock, is actually a logarithmic scale split in two, the top portion going from 1 to \(\pi\) above the C scale, and the bottom portion going from \(\pi\) to 10 below the C scale. This is a convenient arrangement since a standard calculation will be to multiply a constant or gauge mark by one number (\(L\), say) followed by the multiplication of the square of another number (\(B^2\), say).

Consider a cylinder of diameter \(B\) and length \(L\). The initial constant we will need is \(\pi/4\) = 0.7854; however, we measure lengths in inches and we want a result in gallons. So, we really want our constant of interest to be approximately \(\pi/4/277\) = 0.0028. BUT! We will start out the calculation on the D scale, which is the square root of numbers on the C scale, and so we want the square root of our constant: 0.0532. BUT! We will perform the calculation by lining up numbers on the D and C scales which would normally lead to a division calculation. By actually starting out with the reciprocal of our constants above, we can perform a multiplication instead. So, what we will finally need is the mark corresponding to \(1/\sqrt{(\pi/4)/277}\) = 18.78. And this is our starting point.

Close up of “im g” gauge mark with brass pin.
Close up of “im g” gauge mark with brass pin.

One finds that on this Dring and Fage rule there is a gauge mark on the upper D scale at 18.78 which is labeled “im g” next to a brass pin – Imperial Gallons. This is for just this calculation of the volume of a cylinder. The rest of the calculation goes like this: Place the length \(L\) = 40 on the C scale next to the “im g” mark on the D scale. Then find the diameter \(B\) = 32 on the D scale; in our case, it is on the lower D scale. Above this number on the C scale is the answer: 116 gallons. In essence, we start with \(L\) (on C), take its square root (on D), divide by the square root of the reciprocal of our constants, multiply by \(B\) (result still on D), and then square everything which produces the final result on C.


  • Volume of a Cask of First Variety

The previous calculation was for the volume of a cylinder. To find the volume of an actual cask or barrel, we need to perform the reduction of volume by our magical factor within the brackets of our cask equation. For the spheroidal cask this is initiated on the slide rule by use of a special scale marked with an “X” and labeled “1st V”. For this calculation we start by finding the ratio of \(H/B\). Going to the other side of the slide rule, we take the A and B scales and find this ratio in the standard slide rule way. We line up \(H\) on the A scale with \(B\) on the B scale and find the ratio at the “10” mark (or “1” mark) on B. For our example parameters given earlier, we have \(H/B\) = 24/32 = 0.75. We next sight down the slide rule directly below our “10” mark on B to the “X – 1st V” scale, and read off our next number: about 20.3. (A cursor on this slide rule would have been really nice about now…)


Close up of A/B and X scale reading.
Close up of A/B and X scale reading.


Where does the number on this X scale come from? It is the following:

\[ 1/\sqrt{\pi/4\cdot( 2/3 + (1/3)(H/B)^2 )/277} = 20.32 . \]

That is, it is the same as the “im g” mark, but with the spheroidal barrel correction built in. So all one needs to do now is to repeat the earlier procedure for our calculation of a cylindrical volume, but using this number as our initial Gauge Mark rather than “im g”. For example, we place 20.32 on D against the length \(L\) = 40 on C. We then find \(B\) = 32 on D; directly below this number we find the result on C. Doing so, we get the total volume of our spheroidal cask, which is 99.1 gallons, in accord with our earlier computer calculation.


Real casks come in a variety of shapes and so curves were developed for 4 types that resemble the vast majority of cask and barrel geometries. Similar calculations can be performed by using the appropriate X scale for each of the four types. On the slide rule, three other “X”-style scales can be found. Besides the spheroidal First Variety, there is the more common Second Variety (labeled “2nd V”), the Third Variety (labeled “Hs V”, for Hutton’s cask variety), and the Fourth Variety (labeled “Ys V”, for Young’s cask variety). The Gauger would make a few basic measurements of the cask dimensions to see which of the four varieties best described the cask at hand, and then use the corresponding scale for the calculations.

Also, on one edge of the rule, there are three other scales that could be used for this same calculation. One of the three scales is a basic inch scale. Another one, labeled “Sphd” is used in conjunction with the inch scale to determine an equivalent diameter for a spheroid to use in a volume calculation. The third is used similarly for the “2nd Variety”. These scales are found on older rules and pre-date the “X” scales. The technique is straightforward and spelled out in the Officer’s Manual, but the newer X scales were more accurate and easier to use. As the older scales were rarely used by the Gaugers owning this rule, they were relegated to the edge of the slide rule on this model. All of these scales discussed so far are described in more detail in the Excise Officer’s Manual.127


8.32.3 Ullaging a Barrel or Cask

Once the geometry of the barrel is measured and understood, one can then use a “dip stick” or rod to measure the depth of the liquid within the barrel. This can be performed by standing the barrel upright and placing the rod into the barrel through a bung hole in the top until the rod hits the bottom. The interface between the wet and dry portions of the rod indicates the depth of the liquid. Then, one only needs to add up the volumes of our fine segments from the bottom to this interface to get an estimate of the liquid volume. On the other hand, many more barrels were made with bung holes at the central diameter of the barrel, and the rod measurements needed to be made with the barrel lying down. For this case, the math involves a sum of the areas of ellipses and while trickier, also can be estimated in a similar manner as above.

But, to illustrate, let’s do the math for the case of a standing cask of the First Variety. Doing the calculus, we compute the volume of liquid from the bottom of the cask to the top of the liquid – the ullage. We say that the top of the liquid is at the level of \(x = u\), while the bottom of the cask is at \(x = -L/2\). Then,

\[ U = \int_{-L/2}^u \pi b^2[1-(x/a)^2]dx = \pi b^2\left[ x-\frac13(x^3/a^2) \right]_{-L/2}^u \\ = \frac{\pi}{4}B^2 L\left\{ \frac12 \left[ 1-\frac{1}{12}(L/a)^2 \right] + (u/L) \left[ 1-\frac13(u/a)^2 \right] \right\}. \]

Note that if we pull out the first square bracket to the outside of the curly bracket, the new outside factor will be the total volume of our spheroidal cask as found earlier; we’ll call this volume \(V_0\). So, the fraction of this volume filled by liquid will be

\[ U/V_0 = \frac12 + \frac{u}{L} \frac{ 12(a/L)^2 - 4(u/L)^2 }{ 12(a/L)^2 - 1 }. \] Earlier we noted that for a spheroidal cask, \((L/a)^2 = 4(1-(H/B)^2)\), so we can put this into the equation above. Also, it would be much more convenient to measure \(u\) from the bottom of the cask rather than from its mid-point, so we want to re-define \(u \rightarrow u-L/2\). Substituting these two relationships we arrive at the fraction of the cask filled as a function of the ullage measurement:

\[ U/V_0 = \frac12 + \left( \frac{u}{L}-\frac12\right)\cdot\frac{ 1-\frac43(1-x^2)\left( \frac{u}{L} - \frac12 \right)^2 }{ 1-\frac13(1-x^2) }, \]

where \(x \equiv H/B\). And remember, \(u\) is now measured from the bottom of the cask. When \(u = 0\), we get \(U/V_0 = 0\), when \(u=L/2\) we get \(U/V_0 = 1/2\), and when \(u=L\) we get \(U/V_0 = 1\).

Let’s make a plot of our Standing Segment cask calculation, using \(H/B = 0.55\):

UonV0 = function(u,x){ 1/2 + ( u - 1/2 )*( 1 - 4/3*( 1 - x^2 )*( u - 1/2)^2 )/( 1 - 1/3*(1 - x^2) ) }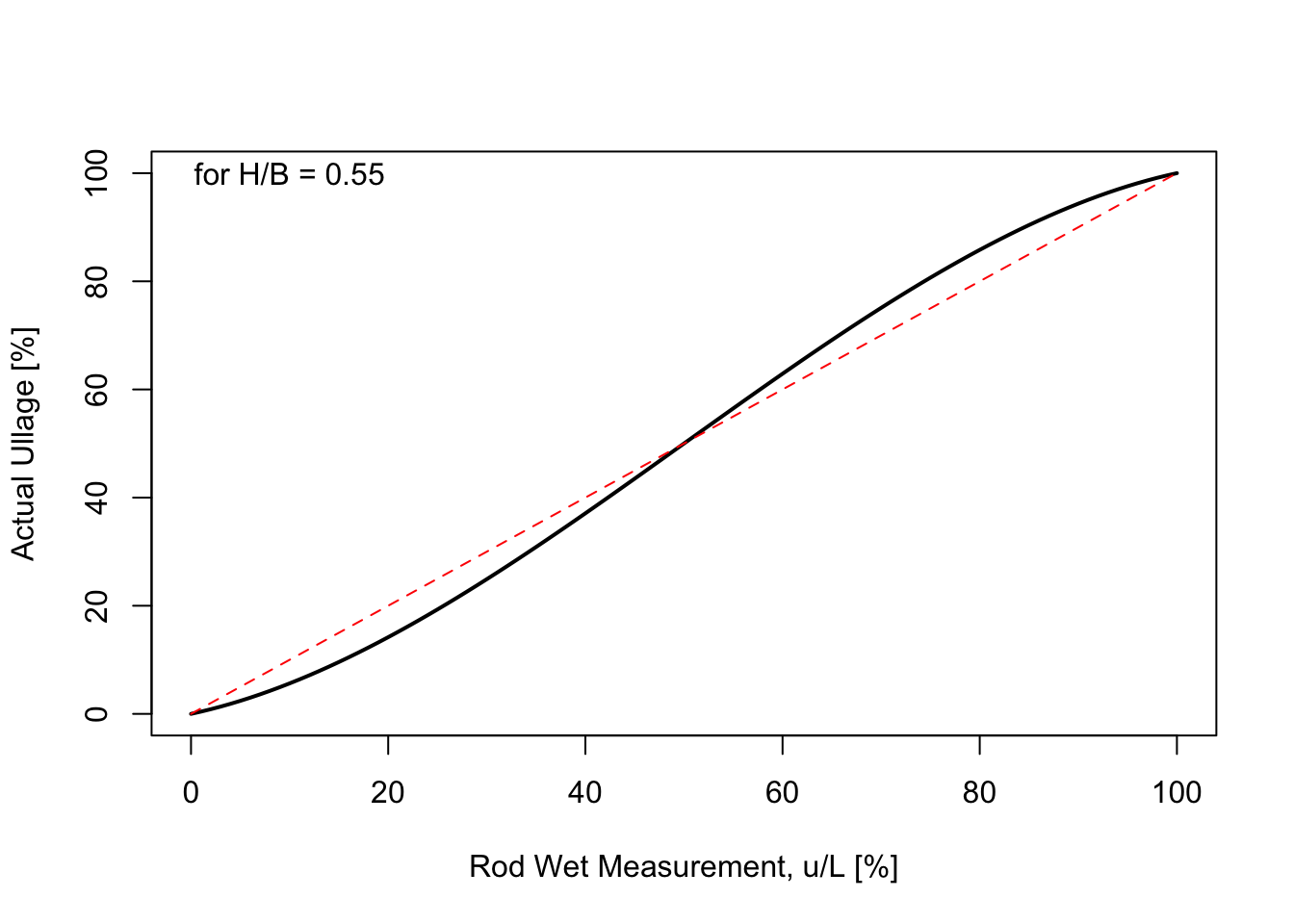

The red dashed line is for comparison with a straight line. We can see how the actual volume of the liquid varies with the depth of the liquid in the cask. In the figure below, we see how this curve depends upon the ratio of \(H/B\) for the spheroidal cask; this variation is observable but not extremely different for a range of ratios. For a value of \(H/B = 0.55\), for example, the variation in volume as a function of depth can be several percent.


To perform a ullage calculation on our Dring and Fage slide rule, the Gauger would use one of two sets of scales. The SS and Seg St scales are actually a single set that is used for ullaging standing casks from measurements made from the head of the cask. The SL and Seg Ly scales are a separate set used for ullaging lying casks from their bung hole. These scale sets are used in conjunction with the B or the C scales to calculate the ullage.

For our standing cask example, with \(L\) = 40 and volume of 99.1 gallons, suppose we measure a liquid depth of 9 inches. The Gauger would place \(L\) on the B scale opposite 100 on the A scale, near the SS scale. Looking at 9 on the B scale he finds 28 on the SS scale and writes this down or remembers it. He then resets the B scale to place 100 against this number, 28, on the A scale. Finding 99.1 on B, opposite this number on A is the ullage in gallons – 27.7 gallons. Using our equations above, I get \(U\) = 26.9 gallons. Note that the SS and SL scales assume a typical cask type and so do not have variations in \(H/B\) built into them.


The Officers and Gaugers using the rule we’ve been examining had to have been proficient in many types of calculations and variations of conditions found in their work. But sometimes when a particular type of cask was always used, then a more particular slide rule may have been used as well. Below is an image of another Dring and Fage excise rule. It is 24 inches in length, and has only 4 scales (the back of the rule is blank): an A scale on the top, B and C scales on the slide (actually the same scale repeated), and a “Seg Ly” scale on the bottom. The A, B, and C scales are all standard two-decade logarithmic scales. Obviously the slide rule is meant to be used to compute the ullage of a lying cask of known volume, and that’s it.



8.32.4 The Malt Depth Scale

Our Excise Officer’s Slide Rule that we’ve been examining has the following 26 scales:

  • A – 3 scales, 2 on one side of the rule, 1 on the other
  • B – 4 scales, 2 on each slide
  • C – 4 scales, 2 on each slide
  • D – 2 scales on one side of the rule, split from 1 to \(\pi\) and from \(\pi\) to 10
  • 2 relic scales on the upper edge for cask volume calculations (plus an inch scale)
  • 2 logarithmic scales on the lower edge, one folded at 1.64
  • 4 “X” scales for calculating volumes for the four varieties of casks
  • a 2-segment SS - Seg St scale, and a two-segment SL - Seg Ly scale for ullaging calculations
  • and a scale marked MD

An examination of the MD scale reveals it to be a simple inverse, or reversed, logarithmic scale running right to left from 2.218 to 22.18. A reversed scale was relatively new to the Gaugers of the mid-1800s. From the 1840 version of The Excise Officer’s Manual, the author Joseph Bateman states, “I cannot ascertain who was the first to adopt this ingenious contrivance to the sliding-rule, but it seems to have been suggested by the remarkable proportions which two equal logarithmic lines bear to each other when one is inverted, or running in a direction contrary to the other.”128

The particular use of this scale was for calculating in one operation the volume in bushels of a rectangular tray of malt barley. The MD scale is what we would today call a folded logarithmic scale, where the fold is at the value of 2.218, which comes from there being 2218.192 cubic inches per bushel. In essence, one dimension would be set on the MD scale (the “malt depth”), against another on the B scale, and the third would be found on the A scale. With one alignment of the slide with the B scale, the calculation can be quickly completed. Note that a gauge mark, labeled MB, can be seen on the A scale at about 2.22, above the 10 on the MD scale: 2218.192 cubic inches per bushel.


Close up of MD scale reading.
Close up of MD scale reading.


Example: Find the volume of a rectangular tray of length 40 inches, width 30 inches, and depth 2.5 inches.

  • Place 40 on B against 2.5 on MD. By 30 on A we read the answer, 1.35 bushels, on B. Check by computer: 40*30*2.5/2218 = 1.3525699.


8.32.5 Proof Calculations

Finally, the point of all of this was to assess tax for the alcohol content of the barrels! And of course to do so, one used slide rules to compute the amount of alcohol in the ullaged liquid and to compute the tax. The specific gravity of the liquid could be determined through the use of an instrument such as a hydrometer. The Sikes Hydrometer was a popular choice, and it came with its own slide rule for computing results.

The percentage of alcohol (ethanol) by volume found in a liquid is expressed in terms of the proof of the liquid. A proof of 100 indicates a liquid that contains roughly 50% alcohol.129 Historically, “proof” was the percentage required for alcohol to ignite or burn; if the liquid ignited, it was proof that alcohol was present. Once things became quantitative, alcoholic beverages were distinguished as being so much over- or under-proof.

In the taxation process, excise taxes were collected based upon a central amount for proof alcohol, and more or less tax for being over or under proof. The slide rule shown in our next image is called a Comparative Rule and was used to compute the assessed tax based upon the determined proof of the alcoholic liquid.

Having determined the proof of the alcohol using a hydrometer system, say, the officer would set the proof mark on the central scale on the slide against the going tax rate for proof alcohol. Then, the tax rate for other values of proof would be automatically aligned accordingly.


  1. Mariam-Webster Dictionary↩︎

  2. Joseph Bateman, The Excise Officer’s Manual, and Improved Practical Gauger, A. Maxwell, 32, Bell Yard, Lincoln’s Inn, London, 1840.↩︎

  3. Ibid.↩︎

  4. Ibid., footnote p. 176.↩︎

  5. In 1800s England, proof was about 1.8 times the percentage of alcohol by volume. Today, in the U.S., the factor is taken to be exactly 2. The definition actually still varies country to country.↩︎