8.37 British Thornton Special Scales
Although specialty slide rules were available as discussed in Special Rules and Scales to perform particular calculations, once in a while one comes across an otherwise standard slide rule but with an unusual set of scales meant to be used for more general calculations. A good example is the Hemmi 153 with its Gundermannian scale and its P and Q scales. The Gundermannian scale is rather specialized to be sure and makes this model very unique. But the P and Q scales, however, make basic calculations of sums and differences of squares faster and more efficient for many applications. Below we discuss sets of scales provided by British Thornton on a number of their slide rule models that also assist in certain calculations and increases the accuracy of others.
8.37.1 Differential Trig Scales
The standard trigonometric scales S and T on a slide rule typically tie the angular measure \(x\) in degrees or radians found on these scales to the value \(\sin x\) or \(\tan x\), respectively, on the C or D scale. And, as can be seen in our discussion of Trigonometric Scales, the spacing of angular measures on the rule becomes quite crowded on the right hand side, particularly where the value \(\sin x\) gets close to one.
The British Thornton slide rule scale set dealt with this issue through the use of their “differential” trigonometric scales, titled Sd/Td and ISd/ITd. The Sd and Td scales are used to compute the sine and tangent of a given angle. The ISd and ITd help determine the angle (or inverse) of a given value for the sine or tangent. The figure below is of the British Thornton Model P221 slide rule. The S and T scales can be found at the top of the front face. On this rule, just below the CI scale one can find, from left to right, the ISd (red) and ITd (black) scales followed by the Td (red) and Sd (black) scales. These last two can be seen just under the cursor in this image, right below the CI scale.

8.37.2 The Sd and Td Scales
The new functions determining the marks along Sd and Td are
\[ {\rm Sd}(x) = \frac{x}{\sin x} ~~~~~~ and ~~~~~~ {\rm Td}(x) = \frac{x}{\tan x}. \] Here, for the British Thornton slide rule, the angle \(x\) is expressed in degrees. If we plot these two functions, we see that for small angles the function is approximately \(180/\pi\) = 57.3 degrees (where the sine of the angle is equal to the angle, in radians, for small angles), but as \(\sin x\) and \(\tan x\) each approach values of 1, the deviations from \(x\) become larger, on the order of \(\pm 50\%\) or so.
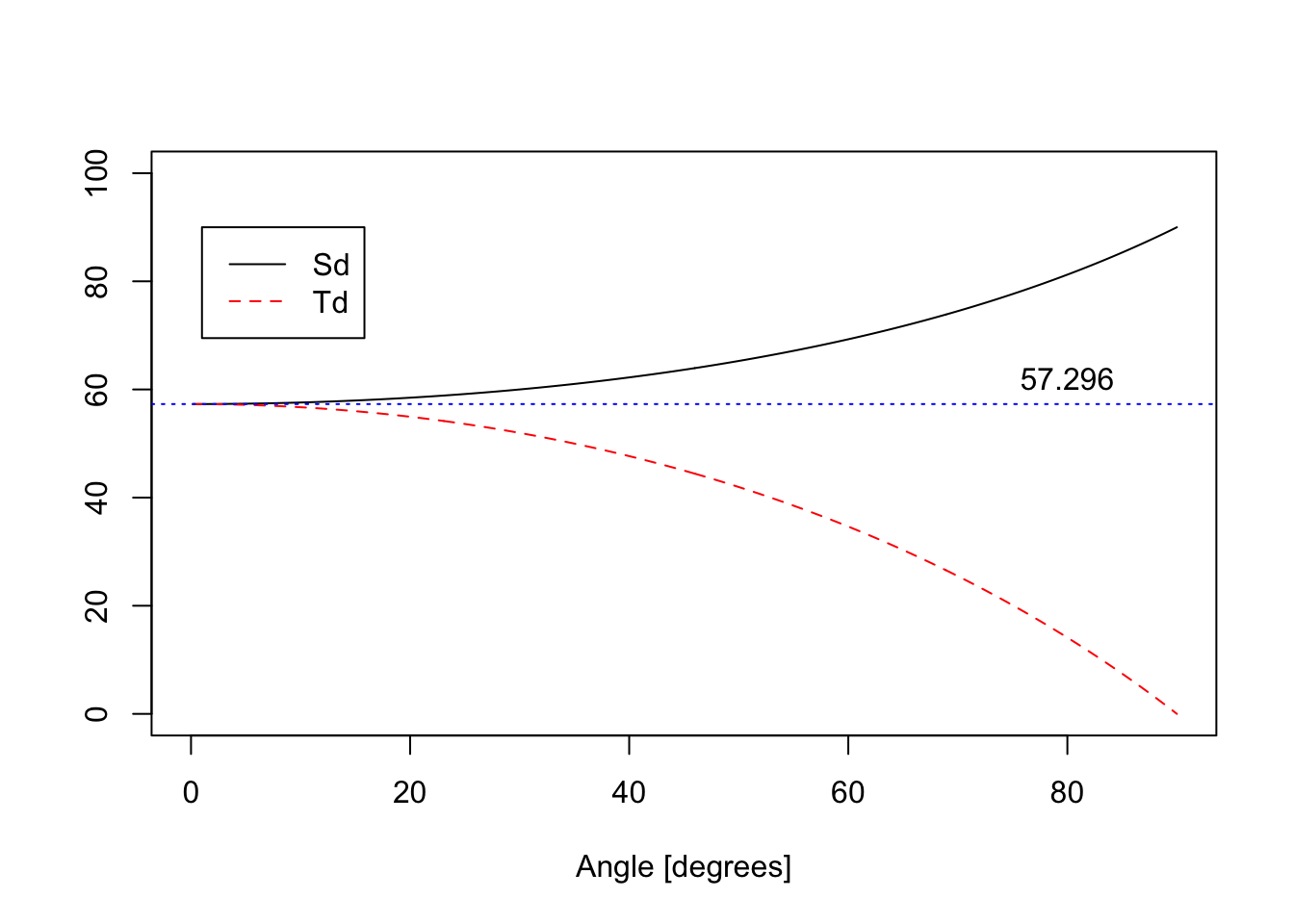
The concept for their use is to put the cursor at the value of \(x\) on the D scale, line up the value of \({\rm Sd}(x)\) on the Sd scale at the cursor, hence dividing, and thus finding \(\sin x = x/{\rm Sd}(x)\) at the index of the C scale. Similarly one finds the tangent using the Td scale rather than the Sd scale. This technique will enable the user to ascertain more precise values of the sine function than can be performed with the traditional scale, particularly at angles closer to 90 degrees, and extends the readings of tangents to beyond the usual 45 degrees of the T scale.
So, by taking the plot above, exchanging the axes, and plotting the new \(x\)-axis with a logarithmic scaling, we can ascertain how to mark the slide for the Sd and Td scales relative to the C scale:
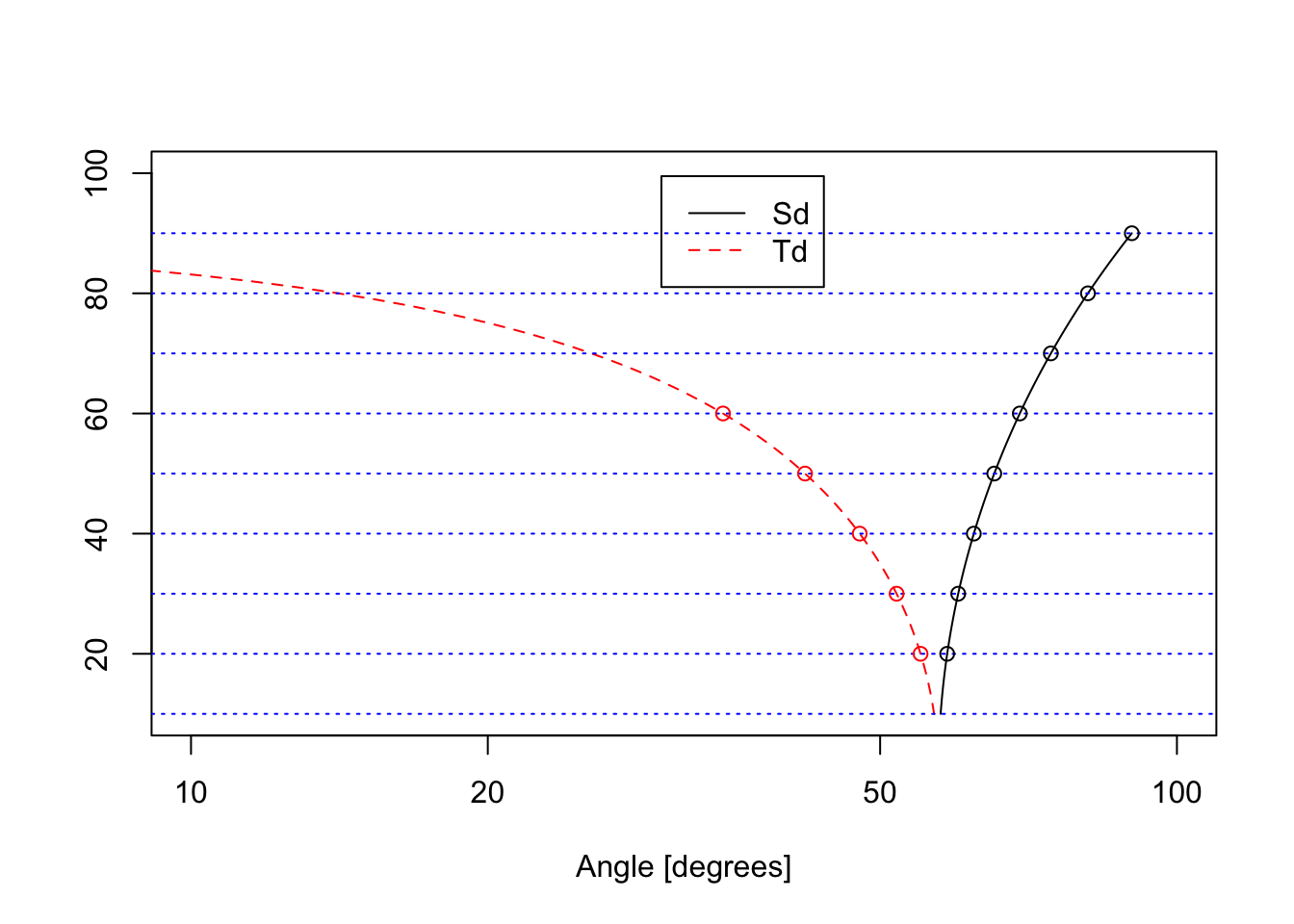
The blue horizontal lines are in increments of 10 degrees, so if we take points at the intersections of our curves with these blue lines, and lay them out along a rule with the spacing given above, we have illustrated the creation of the Sd and Td scales found on the British Thornton slide rule:
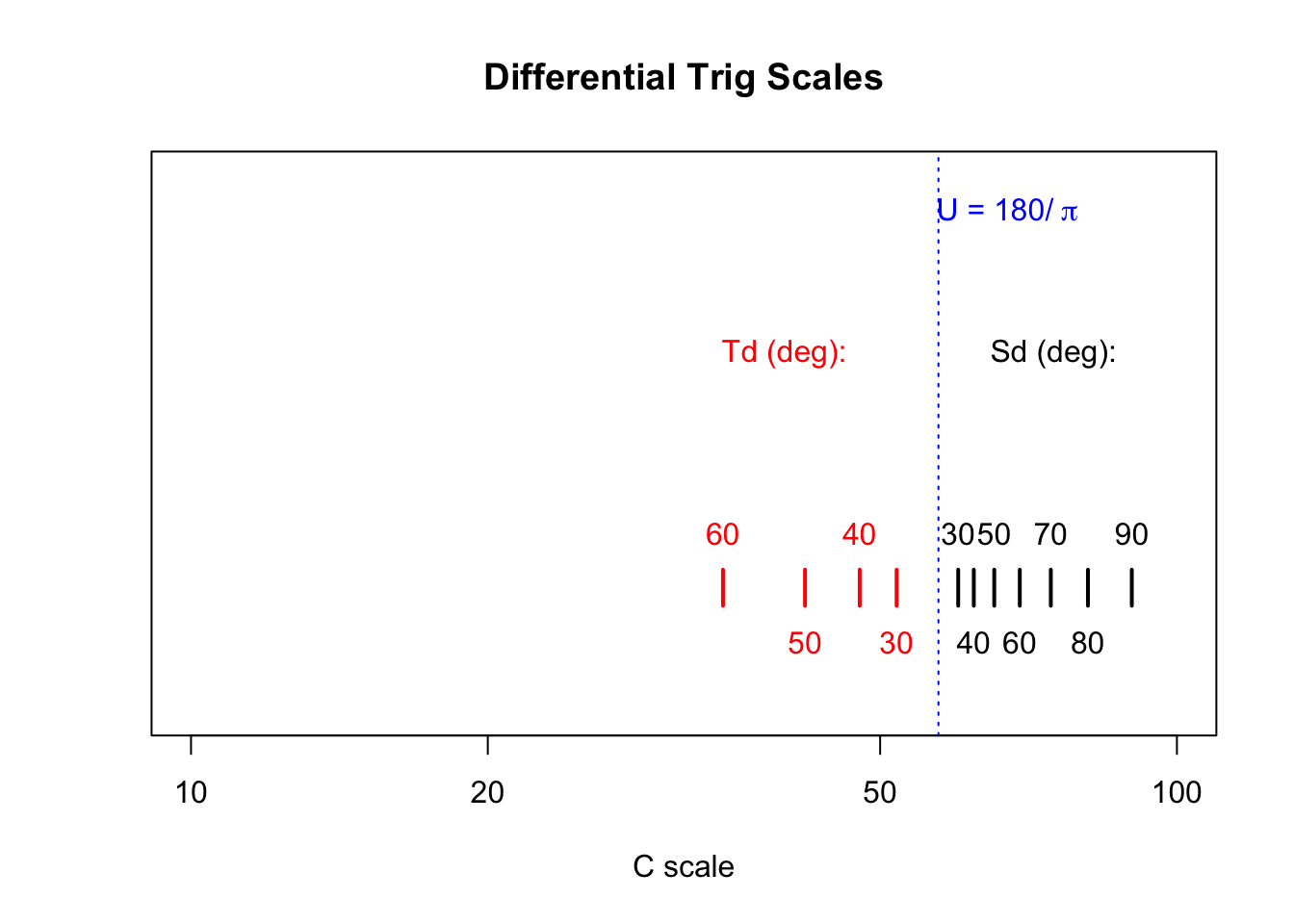
Notice that the two scales/curves converge at the value of U = 57.2958 which is the number of degrees in one radian. Hence, U is labeled on the C scale as a gauge mark.
So now we’ll see how the scales work by going through an example determination of a sine and a tangent. Let’s find the sine and tangent of 58 degrees:
- Traditionally, using the S scale, line up the cursor with 58 degrees on S and read the sine on D: 0.846
- To compare, use the differential scales. Set the cursor to 58 (5.8) on the D scale. Move the slide to line up 58 on the Sd scale at the cursor. The result will be on the D scale under the index of the C scale: 0.848
- By computer: \(\sin(58^\circ)\) = 0.848.
Now imagine one wanted to calculate a quantity like \(r\sin\theta\), where \(\theta\) was 58 degrees and \(r\) was 45.7. With the setting made above, the slide is positioned to do the multiplication right away since the index is set at the sine of the angle. So, sliding the cursor over to 45.7 (4.57) on the C scale we see on the D scale that \(r\sin\theta\) = 38.8.
- By computer: \(45.7\times\sin(58^\circ)\) = 38.7558.
Next, find the tangent …
- First, use the T scale by lining up the cursor with 58 degrees on T and read the tangent on D: Oh! T only goes to 45 degrees!
- So, use the differential scales. Line the cursor to 58 (5.8) on the D scale. Move the slide to line up 58 on the Td scale. The result will be on the D scale under the index of the C scale: 1.60
- By computer: \(\tan(58^\circ)\) = 1.6003.
Again, one can immediately use this result for the next multiplication or another operation as needed.
8.37.3 The ISd and ITd Scales
With the Sd/Td scales alone, it would be difficult to determine an angle given the value of its sine or tangent. Hence, this inverse operation is performed in much the same way as above, but using the inverse scales ISd and ITd found on the rule. The inverse scales are to the left of the Sd/Td scales on the slide of the rule. The inverse functions on the slide are defined as follows:
\[ {\rm ISd}(x) = \frac{x}{\sin^{-1} x} ~~~~~~ and ~~~~~~ {\rm ITd}(x) = \frac{x}{\tan^{-1} x}. \]
As with the Sd/Td scales, the ISd/ITd scales are used in conjunction with the D scale as follows. Suppose we know that the sine has a value \(x\); put the cursor at \(x\) on the D scale. Find the same value \(x\) on the ISd scale and move this to the cursor, hence dividing. Thus, we can find the value of \(\sin^{-1} x = x/{\rm ISd}(x)\) at the index of the C scale. Similarly use the ITd scale to find an inverse tangent.
Since Sd/Td scales involve operations in units of degrees, then when performing the inverse operations we want the final answers to be in degrees as well. Hence, the units for ISd and ITd will be “inverse degrees” (i.e., 1/degrees) if we want the resulting \(\sin^{-1} x\) and \(\tan^{-1} x\) operations to result in degrees.
Plotting the inverse functions we find
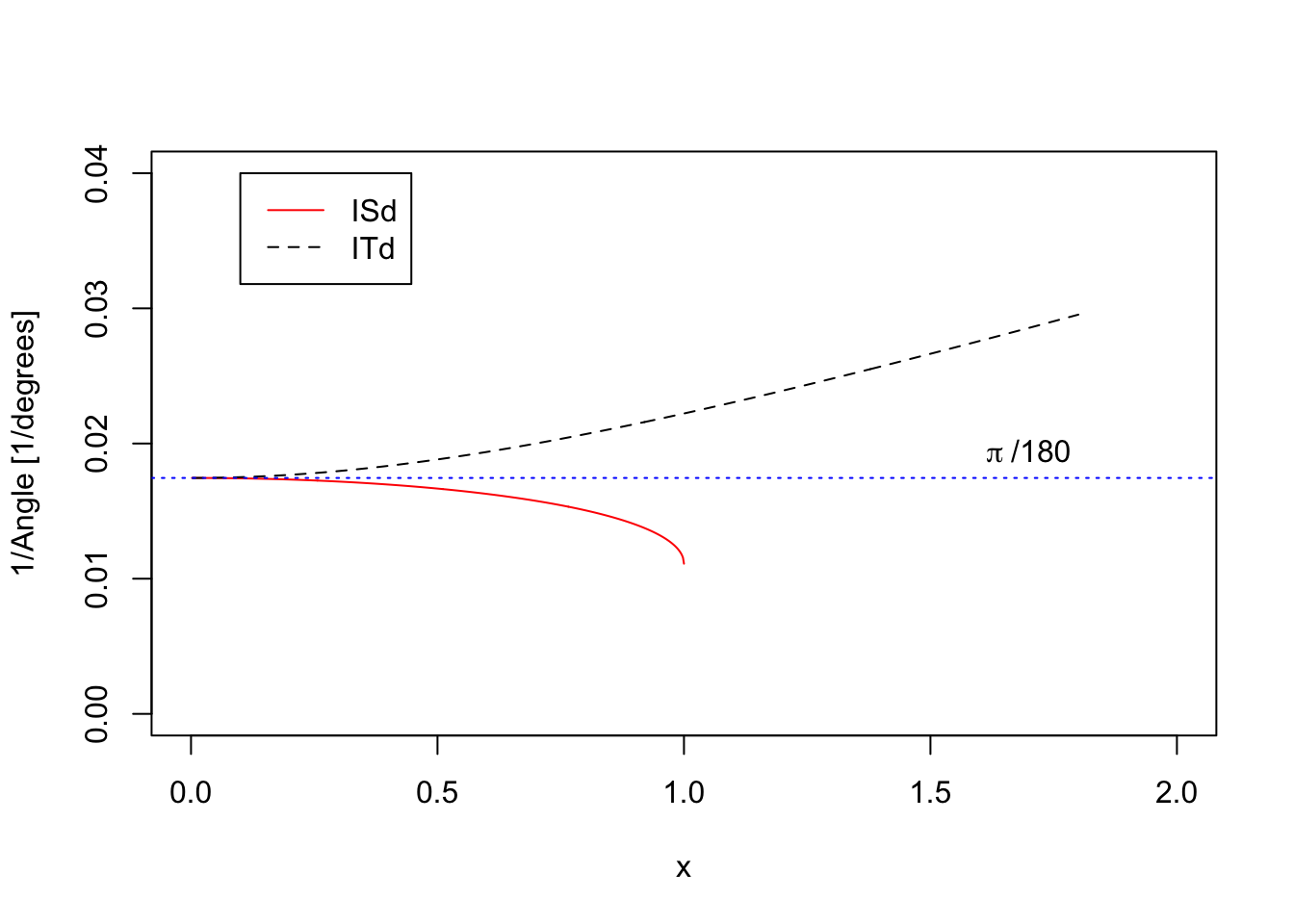
and, as before, by switching the axes and using a logarithmic plot on the horizontal scale we arrive at:

Again, picking out a few representative values along the vertical axis, and laying them out on the slide with the spacing given above, we can illustrate the creation of the ISd and ITd scales found on the British Thornton slide rule:
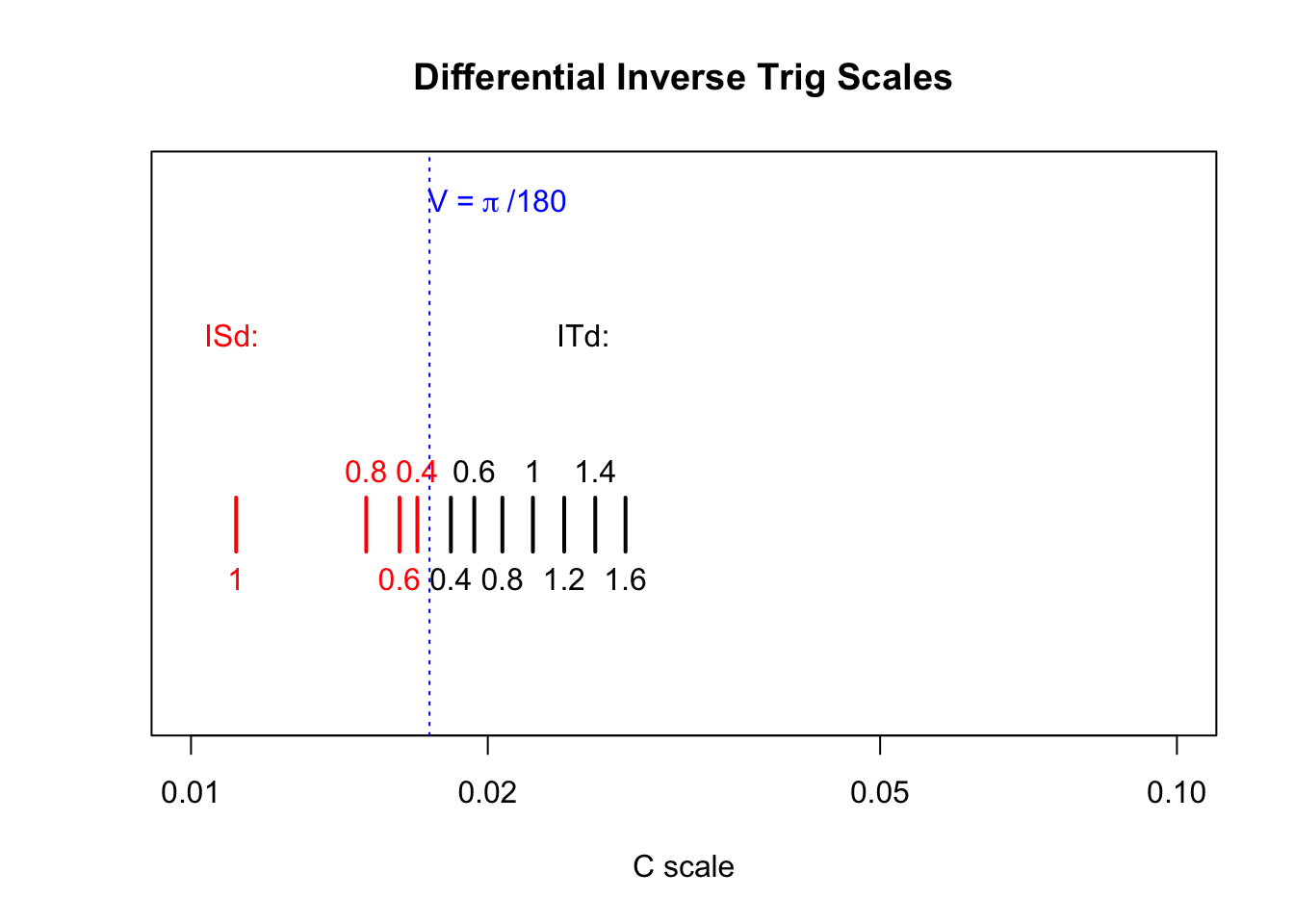
We see that another useful gauge mark appears at a value of V = 0.0175 on the C scale, which is the number of radians per degree.
It is important to point out that when reading the values of Sd/Td on the C scale, the indices on the C scale are at 0.1 and 1. When reading the values of ISd/ITd on the C scale, the indices on the C scale are at 0.01 and 0.1. But, luckily, one really doesn’t have to worry about this when simply using the scales. The values of the sine and tangent will be read between 0.1 and 1 (or maybe up to about 2 for the tangent on these scales), while the angles will always be read in units of degrees with values between 10 and 100.
Some examples help to illustrate the use of the inverse scales. Let’s find the inverse sine and inverse tangent of 0.99:
- Using the S scale, line up the cursor with 0.99 on the D scale and read on S the angular value: somewhere around 80 degrees…
- To compare, use the inverse differential scales. Set the cursor to 0.99 on the D scale. Move the slide to line up 0.99 on the ISd scale at the cursor. The result will be on the D scale under the index of the C scale. I find 81.8 degrees.
- By computer: \(\sin^{-1}(0.99)\) = 81.8904.
Next, find the inverse tangent …
- Use the T scale by lining up the cursor with 0.99 on D and read the angle on T: 44.7 degrees
- Next, use the inverse differential scales. Line the cursor to 0.99 on the D scale. Move the slide to line up 0.99 on the ITd scale at the cursor. The result will be on the D scale under the index of the C scale: 44.7 degrees
- By computer: \(\tan^{-1}(58^\circ)\) = 44.7121 degrees.
The Td and ITd scales are especially useful for angles in the range between 45 \(\lt\) \(\theta\) \(\lt\) 60 degrees.
8.37.4 Pythagorian Scales
Referred to as “Vector Analysis Scales” in the British Thornton instruction booklet, the Ps and Pt scales are most commonly used for finding a side of a right triangle given the other two sides. The Ps scale is identical to the “standard” P scale found on the German Darmstadt slide rules. Given the hypotenuse of a right triangle and one side, the value of the other side can be computed in a straightforward manner. The Pt scale completes the set by easily computing the hypotenuse given both of the other two sides.
Mathematically, the Ps scale is \[ Ps = \sqrt{1-s^2} \] and so if s represents the sine of an angle, then Ps will give its cosine. It can also be used to find the difference of squares of two numbers, as follows.
To compute \(b = \sqrt{c^2 - a^2}\) given \(c\) and \(a\), first re-write the equation as \(b = c\sqrt{1-(a/c)^2}\). (Notice that \(a/c\) is the sine of the angle opposite of \(a\).) We use the C/D scales to compute \(a/c\), and then taking this result, move the cursor to this same value on the Ps scale. After setting the index of the C scale to the cursor, now move the cursor to the value of \(c\) on the C scale and read the final result on the D scale. Example: Let \(c\) = 5 and \(a\) = 4.
- Using C/D, find 4/5 and slide the cursor to the index on C to find 0.8 on the D scale.
- Place the cursor to 0.8 on the Ps scale. Move the C index to the cursor.
- Slide the cursor to 5 on C scale. The answer will be on the D scale: \(b\) = 3.
The complementary Pt scale provides \[ Pt = \sqrt{1+t^2} \] and, if \(a\) and \(b\) are the two sides of a right triangle, then the tangent of the angle opposite \(a\) will be \(\tan\theta = a/b\). The hypotenuse will be \(c\) = \(b\sqrt{1+(a/b)^2}\) = \(b\sqrt{1+\tan^2\theta}\), hence the name of the scale. Example: Let \(a\) = 3 and \(b\) = 4.
- Using C/D, find 3/4 and slide the cursor to the index on C to find 0.75 on the D scale.
- Place the cursor to 0.75 on the Pt scale. Move the C index to the cursor.
- Slide the cursor to 4 on C scale. The answer will be on the D scale: \(c\) = 5.
The P scale on the Darmstadt rules and the equivalent Ps and its sibling Pt scales on the British Thornton rules became very popular in Europe. In the USA, on the other hand, students were typically taught to perform the same calculations using the standard C/D and A/B scales by the technique described in Squares and Square Roots, where one adds or subtracts “1” during the computation on the A scale. The “P” scales typically were not found on the popular US-produced slide rules.