1.3 Multiplication and Division

Suppose we have two numbers, \(x\) and \(y\) and we wish to multiply them together. If we write each of them in terms of exponents \(p\) and \(q\), such that

\[ x = 10^p~ \\ y = 10^q, \]

then

\[ x\times y = 10^p \times 10^q = 10^{p+q}. \]

From the above, and from our definition of a common logarithm, we see that

\[ \log x = p~ \\ \log y = q, \] and

\[ \log(x\times y) = p+q. \]

Thus we see that the logarithm of \(x\times y\) will be the sum of the exponents \(p\) and \(q\), which are themselves the logarithms of the original numbers. This gives the very important general result:

\[ \log (x\times y) = \log x + \log y. \]

Adding the logarithms of two numbers gives the logarithm of the product of the two numbers!

As for division, we remember that this is just the inverse of multiplication. Suppose that our above multiplication gives the result \(x\times y=r\). If we want to solve \(r \div x\) we should get \(y\):

\[ r \div x = \frac{r}{x} = \frac{x\times y}{x} = y. \]

We see, then, that

\[ \log(r\div x) = \log y \]

but since \(\log r = \log(x\times y) = \log x + \log y\), then we get the general result:

\[ \log(r\div x) = \log r - \log x. \]

That is, to divide two numbers, we subtract their logarithms and find the number whose logarithm is that result.

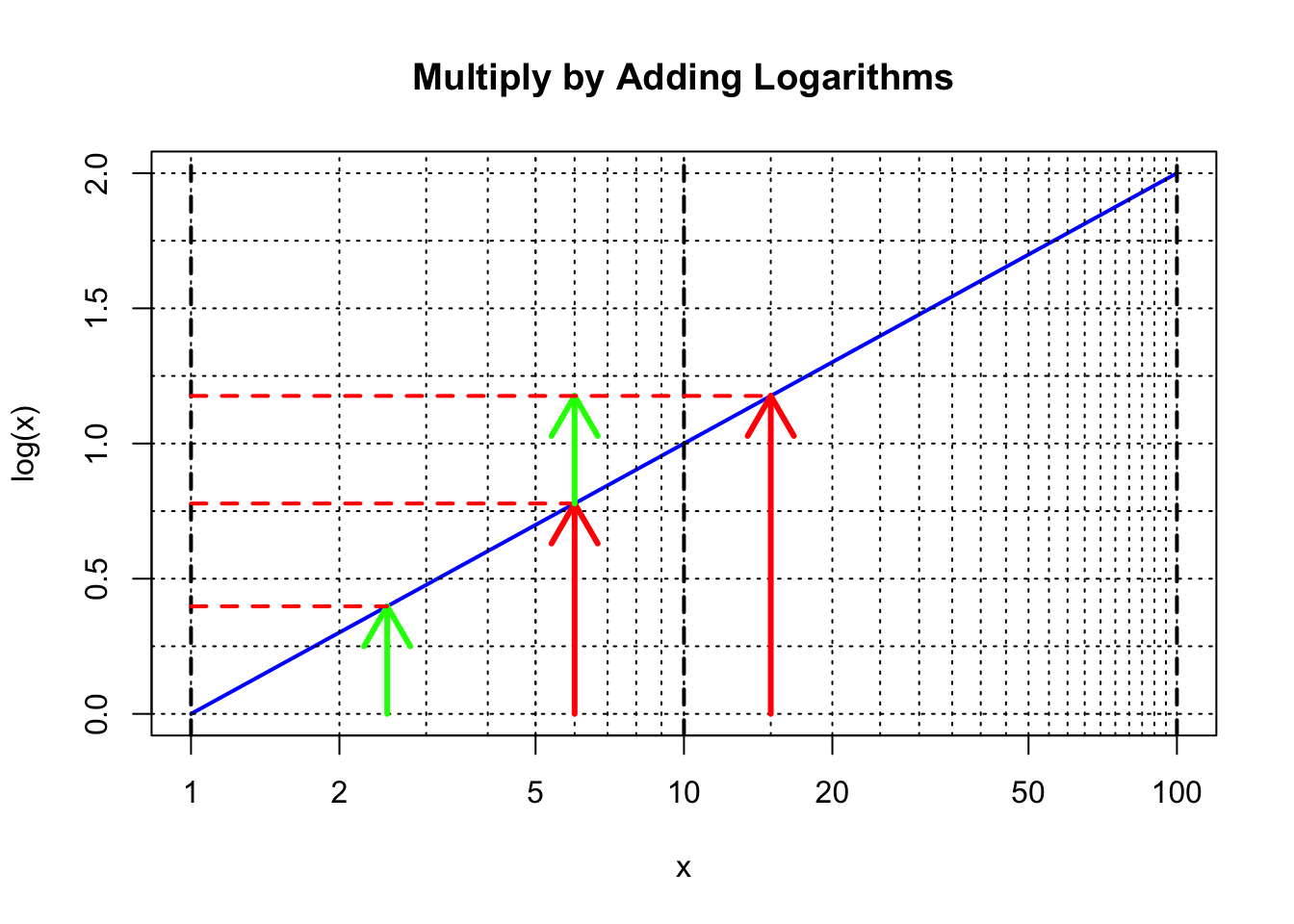
The basic operations of the slide rule involve adding and subtracting distances along the rule, distances which are proportional to the logarithms of the numbers on the scales. Our “logarithmic scale” gives us distances along the horizontal axis that are proportional to a number’s logarithm. We see in the plot below, for example, that adding the logarithms of two numbers, let’s say 2.5 and 6, gives us the logarithm of their product – in this case, 15: