8.8 Rules of Engravement
With today’s modern personal computers it is straightforward and quite ordinary to be able to create professional-looking documents for printing and distribution. Numerous columns of perfectly justified text, headlines with various font sizes, carefully cropped photos and other images, and content that runs across multiple columns and pages require just a few clicks of the mouse and strokes of the keyboard. The common “What You See is What You Get” (WYSIWYG) software of today makes quality design and layout of books, reports, and newsletters accessible to everyone.
But consider the creation of a magazine or newspaper page in the old days. While I cannot speak about modern techniques with authority, I can speak a little bit about the “old days” as I worked on a small newspaper in the early 1970’s. Creating a layout of a newspaper page meant, actually, laying out items on a table, cutting columns of pre-typed text and pasting them into position on the layout page, typically using wax, so that they could be taken up and moved or re-centered. This is where the term “cut and paste” comes from. The standard newspaper page would have a certain number of columns of a particular width, and the text was typeset so that each line was justified to that width. This meant that each article had a length measured in lines or, equivalently, a certain number of “linear inches” of text. Thus, the length of an article in column inches or just “inches” is important.
The entire page, on the other hand, will have a certain number of columns, separated by a certain amount of empty space, along with margins of a certain width or height around the perimeter of the entire page. As every piece of available space on the page is important, lengths that were subdivisions of an inch were necessary; the pica was the length used in the typesetting industry, where 1 inch is approximately 6 picas, while a point is 1/12 of a pica. (The exact dimension of a “pica” varies somewhat in the industry.) A column might have a width of 2.25 inches = 13 picas 6 points, for instance, and columns might be separated by a few picas. The size of the text itself was determined by the font used, which could have different sizes. One might choose a 10 point font or a 12 point font, with a certain number of points used between lines of text. A standard 12 point font with leading (extra spacing between lines to make more legible; pronounced “LEDD-ing”) would result in 14 points per single-spaced line. Text justification, line counts, and, very importantly, the inclusion of images into the text required fairly precise numerical computations to be performed during the layout process.
For example, how would properly sized photographs be introduced into newspapers before computers? An etched negative of the photo was created on a surface, using a process called photoengraving. Starting with a glossy photograph typically of a standard size such as 8 inches by 10 inches, a lens system would be used to focus an image of the photograph with the desired final size onto a metal surface that was coated with a photoresist material. The photoresist would become hardened where it was hit by light, while the dark areas remained soft. Excess soft photoresist would be removed using a solvent, and what remained would be a raised negative of the desired image etched onto a plate which could then be used for printing on a printing press. All of this would be done by the print shop, but the the print shop had to be provided with the original print of the photo for reducing, along with instructions for how much to reduce the image to fit the desired space on the layout page.
The standard slide rule is a perfect instrument for doing proportions calculations. For example, take the calculation of 4 divided by 5, which is 0.8, or 80%. To perform the calculation on a standard slide rule, the 5 on the C scale would be set to the 4 on the D scale, with the result read on the D scale below the end of the C scale, as shown in the following figure:

But note that other combinations read along the C/D scales will also yield the same “final answer”. For example, 3.2 divided by 4, or 6 divided by 7.5, etc., all yield an “answer” of 80%. If we had a rectangular picture of dimensions 4 high by 5 wide, then a reduction in its height to 3 would require a reduction in its width to 3.75 to maintain the same proportion, as can be found on the setting above.
Special slide rules – often called proportion rules or engraving rules – were available for ease of computations in layout and printing environments where the more “standard” slide rules were not so commonly used. Basically, such rules simply divide two numbers in the standard slide rule way using two sliding logarithmic scales. If one sets the ratio on the two scales to \(a/b\), then any other two numbers read opposite each other on the two scales will have the same numerical ratio. One simple slide rule for such a calculation is shown below, sold by Arthur Brown and Bro., Inc., in the 1920’s.

The Lawrence Engineering Company made several rules for this purpose, such as the Model 10-C Engraver’s and Photographer’s Proportion Calculator and the Model 10-N Printer’s Proportion Rule shown below. Art supply stores often sold similar slide rules without manufacturers’ labels, but perhaps with the store’s advertising printed on the rule.


Our next image, below, is of a proportions rule that was likely used at a major newspaper or magazine company, or perhaps at a print shop. There is no indication of the maker of the rule, but it is a laminated wooden rule and has a cursor for accurate readings. The scales have about twice the spacing as those on the earlier examples and so give higher accuracy in the results. They are labeled A, B, P, L, and C, but they have little or no relation to the standard slide rule scales by the same names. On this particular rule, A and B are used to set a ratio, “\(A/B\)”, and the result (in terms of “percent reduction”) is given on the C scale, \(C=A/B\times 100\). The P scale – presumably for “picas” – is found both on the slide of the rule and on the bottom stock of the rule. These P scales yield 6 times the number found on the B scale or A scale, respectively. And the L scale found on the slide gives 14 times the number on the B scale, though I have not yet been able to verify the purpose of this scale (14 points per Line?). Since there is a P scale on both the slide and on the stock, ratios of larger numbers can be obtained by using these two P scales against each other, just as one could use the A/B scales, and the percent reduction from the P scale ratio also can be read from the C scale.

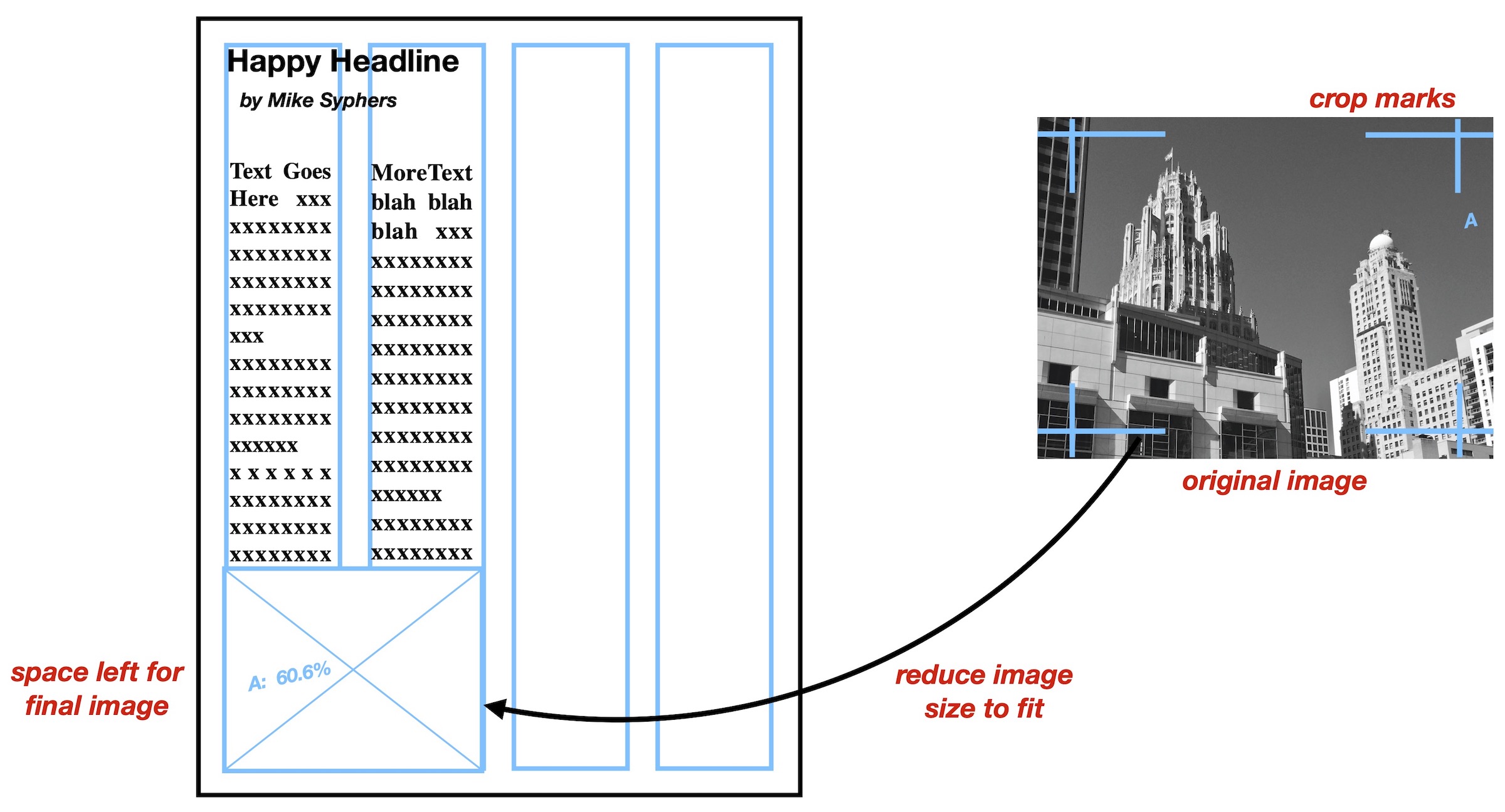
Suppose a photographer provides a newspaper with an 8x10 black and white photograph (8 inches tall, by 10 inches wide). An editor may wish to crop the photo in order to produce a better image for the story at hand, and the resulting cropped portion of the photo ends up, say, 6.5 inches by 8.25 inches. Note that to maintain as high a resolution for the final photograph as possible, one always tries to use larger images that are then reduced to their final size. Cropping the photo is performed by using a blue grease pencil and creating “crop marks” on the glossy photo to indicate the corners of the desired final image. (In the engraving process, the printer uses a filter to make blue marks created by the editors invisible.) Further suppose that the final photo must span a width of two columns – say 2 \(\times\) 2.25 inches plus 3 picas (space between columns) = 5 inches = 30 picas. The editor needs to determine by how much to reduce the size of the photograph to fit within the two column width, and simultaneously figure out how many vertical inches or lines of text will become occupied by the photo.
Using the above proportion rule, we want to scale the cropped photo from 8.25 inches wide to 5 inches wide. So we set the original width of 8.25 inches on the A scale opposite the new width of 5 inches on the B scale (upper red arrow). The percent reduction is read off of the C scale just above the right tick mark (lower red arrow). We see that the photograph needs to undergo a reduction by a factor of 60.6%.26

This number would be written on the back of the photo, as well as on the layout page (again, using blue pencil), so that the print shop could make the appropriate scaling when creating the final engraving. Keeping the previously found ratio set on the slide rule, by moving the cursor to 5 on the A scale (upper blue arrow) we can also see that the height of the resulting photo will be 3 and 1/32 inches, as read on the B scale. Following the cursor to the P scale we can also read the desired height in picas (about 18.3, or about 18 picas 4 pts). Using this information, the appropriate vertical space on the page can be marked off so that the text of the article can be pasted onto the layout page outside the region reserved for the photograph.
Slide rules such as those shown above are prefect tools for computing proportions. Setting a single ratio on the rule, any other combination of numbers with the same ratio can be read off at a glance. These rules were surely great time savers in the layout rooms of newspapers and magazines, as well as in the print shops and photo shops of the era. In fact circular “proportional scales” and dials are still for sale online, and can sometimes be found in art supply stores even today.
\(- 30 -\)
Slide rule aficionados will note that the same “answer” is found on the B scale under the 10 on the A scale.↩︎