2.1 A Word About Bases
If we make plots of \(b^x\) for various values of \(b\) we can see that the curves all look very similar in nature:
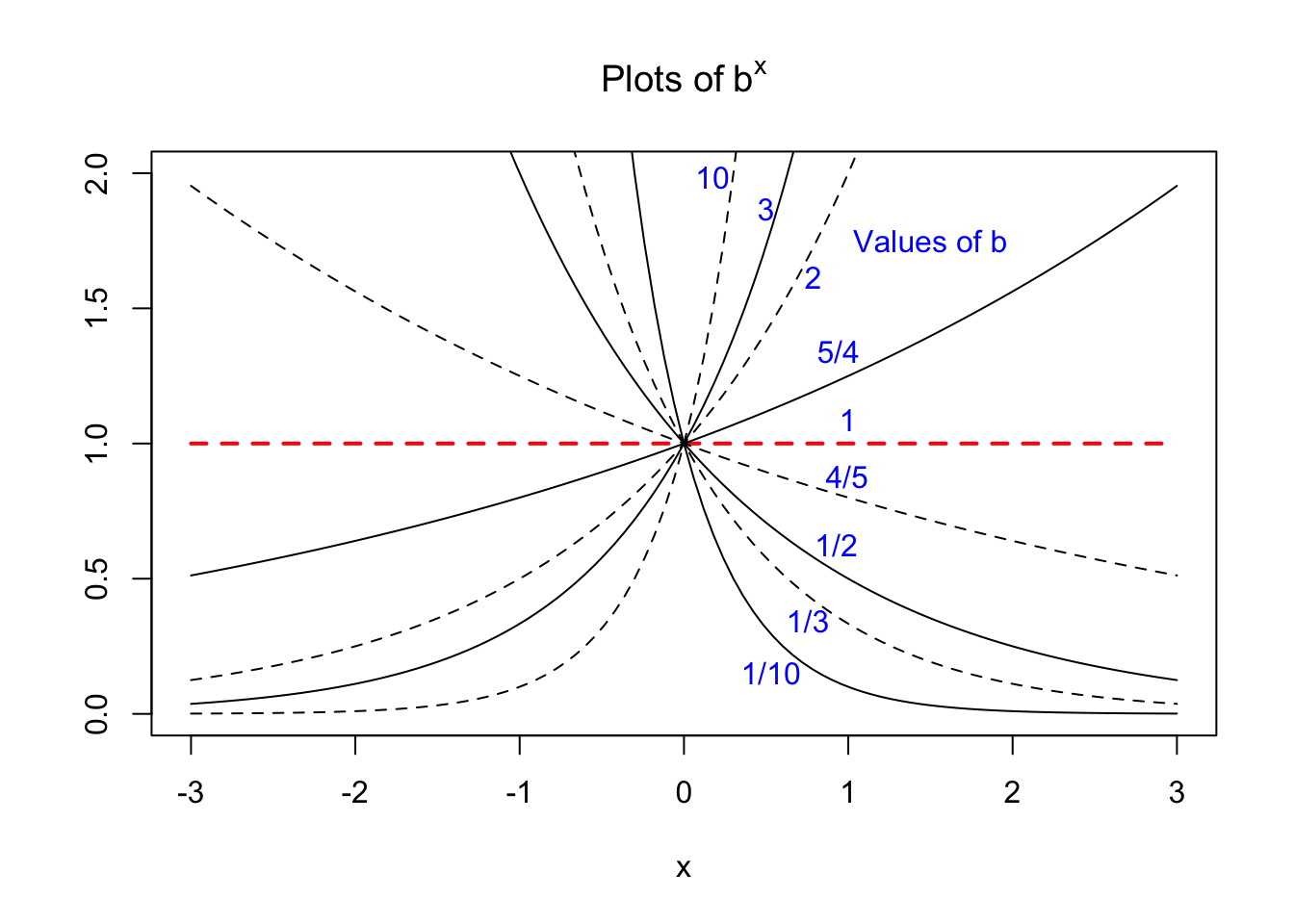
The above plot emphasizes that for any base \(b\), \(b^0\) = 1 and \(b^{-x}\) = \((1/b)^x\). Let’s draw a horizontal line across a similar plot, say at a value of 3.5, and look at where it intersects a few of our curves:

The above figure illustrates how the number 3.5 can be represented by any base raised to a particular power. As particular examples,
3.5 = \((0.5)^{-1.8074}\) = \((0.333)^{-1.1403}\) = \((0.1)^{-0.5441}\),
and
3.5 = \((2)^{1.8074}\) = \((3)^{1.1403}\) = \((10)^{0.5441}\).
Obviously, if we were to choose a different value for our base \(b\), then we could see where its curve crosses the line at 3.5 and hence know the logarithm of 3.5 (the exponent, \(x)\) for that particular base.
To see how the various choices of base are related, take the operation \(b^x\) and suppose we wish to write this in terms of a new base, \(a\). That is, suppose \(a^{x'}=b^x.\) Then finding the logarithm for base \(a\) on both sides we find that
\[ \log_a a^{x'} = \log_a b^x \\ x'\cdot \log_a a = x\cdot \log_a b \\ ~~~~~~~~~~~~~ x'=x\cdot \log_a b \] or, in other words,
\[ a^{x\cdot \log_a b } = (a^x)^{\log_a b} = b^x. \]
We saw another version of this result earlier, since if \(y = b^x = a^{x'}\) then we can identify \(x=\log_b y\) and \(x'=\log_a y\), yielding \(\log_b y = \log_a y / \log_a b .\)
So we see that \(b^x\) is the same as \(a{^{x'}}\) with a special scaling of the argument, namely \(x'= x\times \log_a b\). But is there a natural choice for a particular base number, and its logarithms, from which all other exponential functions should be scaled?
Our quest below will be to find a natural definition for a logarithm and to determine its natural base, then show how to compute values of logarithms for that base. Once this is done, we can find the logarithm in any other base through the general rules that any logarithm must obey. This will also give us the tool needed to directly compute the value of any number taken to any arbitrary power.